Questão 4: Considere a EDP do calor, sendo :
Onde está descrita no item a seguir:
- Mostre a função , como sendo a extensão ímpar e periódica de período da função , que está definida em e esboce seu gráfico no interior de , usando o fato de que , com .
- Calcule a série de Fourier da função dada no item .
- Usando os resultados dos itens e , calcule (mostrando os detalhes) a EDP do problema acima usando o método de separação de variáveis.
Passo 1
Vamos aqui desenhar a função para a gente ganhar uma noção visual de quem vai ser a função , já que essa última vem por construção em cima da função :
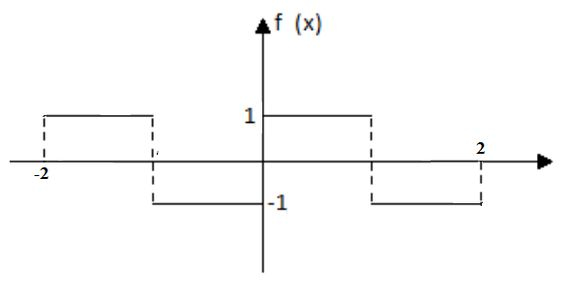
O problema nos pede uma função de extensão ÍMPAR e PERIÓDICA da função . Vamos com calma, ok?
Passo 2
Para uma função ser ÍMPAR, o que na matemática significa:
Precisamos ter uma reflexão ao redor da origem dessa forma aqui:
Literalmente como se girássemos o plano ao redor da origem, saca? (se não saca dê uma olhada nessa comparação legal )
E mais! Para uma função ser ímpar, ela precisa estar definida na origem, afinal á única forma de isso acontecer é se !
Prontinho! Criamos uma função que veio da , a diferença agora é que essa é Ímpar. Em notação matemática temos isso aqui:
Como ...
Saca?
Passo 3
Mas calma que ainda não acabamos de definir a função ! Ela também deve ser periódica de período igual a , ou seja:
ESSE é o gráfico da que o problema nos pediu! Sua notação é:
Significa que a cada ela começa a se repetir, saca?
No mesmo item , foi pedido para a gente que desenhasse o gráfico da função no interior de , e a boa notícia é que já foi desenhado no passo :
Passo 4
A série de Fourier de uma função qualquer periódica de período é assim:
Onde os termos e se calculam assim:
Como queremos representar uma função de extensão ímpar, os termos zeram! Logo, só temos que calcular o ...
E mais! Para uma função ímpar, a integral de a é dá o mesmo valor de a , então a gente pode simplificar ainda mais o calculo:
Então vamos calcular esses termos !
Passo 5
Como é o Período da nossa função, sabemos que o período da nossa função , então...
Além disso, para ...
UAI! O que é ? Se você se recordar que é um número natural que varia de ao ...
Então...
Logo, voltando para a tarefa de obter da série de Fourier de ...
O que é quando é par , e quando é ímpar , então só vai sobrar os termos ímpares ...
Chamando de novamente (é apenas um nome):
Retornando para a série de Fourier:
Lembre-se que só sobraram os termos pares, em outras palavras ...
Passo 6
O método de separação de variáveis é o método que você chuta a solução, como sendo um produto de soluções de variáveis isoladas. Tipo, no nosso caso, a solução é , e vamos falar que é a mesma coisa que um produto de uma função só de por outra só de :
Saca? Agora que vem a graça do problema, se essa é uma solução então ela satisfaz a equação da EDP...
O legal disso é que, por exemplo, em , a derivada é com relação a , como , independe de , então...
Nas duas parcelas, como estamos derivando em relação a uma única variável, essa é uma derivada comum, entende? Tipo ...
Repare que como temos coisas independentes, podemos separar esses caras, ou seja, jogar tudo que tem por um lado e tudo que tem por outro. Veja:
Quase pronto! As variáveis estão até separadas, mas falta mais uma coisinha: como são possíveis duas funções de duas variáveis diferentes serem iguais? A única solução é que elas sejam ambas iguais uma constante, que não depende nem de uma e nem de outra, saca?
O menos na frente da constante serve apenas para simplificar um pouco as continhas, mas você pode chamar simplesmente de , ou , ou qualquer outro nome de constante que tiver em mente . Assim...
e
Passo 7
Separamos as variáveis na EDP, mas no nosso problema, existem outras condições que envolvem a nossa ...
Olhando para as condições de contorno:
Substituindo a nossa solução...
Nos dois casos, vamos considerar que , pois se não a gente recai na solução trivial da EDP, ou seja...
Então, pela condição de contorno...
Já pela condição de temo inicial...
Assim, podemos separar agora a nossa EDP, em duas EDO’s:
Veja que a primeiro podemos resolver a primeira EDO, já que dela temos muitas informações de condição de contorno ! Vamos nessa?
Passo 8
A gente pode resolver essa EDO, por equação característica, afinal é uma constante...
Só que veja que aqui temos que ter cuidado! Não conhecemos lambda, então temos que supor cada caso, se lembra?
- Para Lambda menor que ():
- Para ...
- Já para ...
A solução será real e vai ser do tipo...
Aplicando as condições de contorno...
Logo, isolando em cima e substituindo em baixo, ganhamos...
Nesse caso, como a exponencial nunca é zero, então...
Essa é a solução trivial que a gente não quer, logo não pode ser menor que .
Aplicando as condições de contorno...
Novamente temos a solução trivial!
O que está dentro da raiz é negativo, então a gente tem uma solução aparentemente imaginária! Mas se você se recordar um pouquinho de EDO’s, vai ver que essa resposta é real dessa forma aqui:
Onde
Logo, a solução será do tipo...
Aplicando as condições de contorno...
Se , temos a solução trivial de novo, mas dessa vez o pode ser diferente de , tudo que precisa acontecer para isso é...
Logo...
Esse é o autovalor da nossa ! E a autofunção é
Encontramos uma solução que não é trivial! . Segura ela aí, então e vamos embora!
Passo 9
Bem, agora que temos um conjunto de valores de que não dá uma solução trivial, a gente pode seguir com a solução indo agora para a segunda EDO:
Resolvendo por separação de variáveis, essa EDO...
Lembrando que , e chamando de constante (é só um nome)...
Passo 10
Veja que temos um conjunto de soluções desse tipo aqui:
Considerando
Logo, a nossa solução geral vai ser a soma de todas essas soluções e múltiplos delas...
Quem é ? Bem, para isso podemos olhar a última condição que não utilizamos para nada: a condição inicial!
Então venha comigo mais um pouco (tá quase acabando! ).
Passo 11
Veja que então é então os mesmos termos da série de Fourier da extensão ímpar que calculamos...
Se considerarmos então apenas os termos ímpares (os pares são )...
E essa é a solução final!!!