Determine a extensão ímpar periódica de período da função para esboçando o gráfico no intervalo
Encontre a série de Fourier de senos da extensão ímpar periódica da função para
Resolva o seguinte problema de valor de contorno usando o método de separação de variáveis justificando cada passo detalhadamente:
Passo 1
Vamos começar fazendo o gráfico da função estendida, para a gente poder visualizar melhor a questão, ok? Primeiro, vamos desenhar os dados do enunciado:
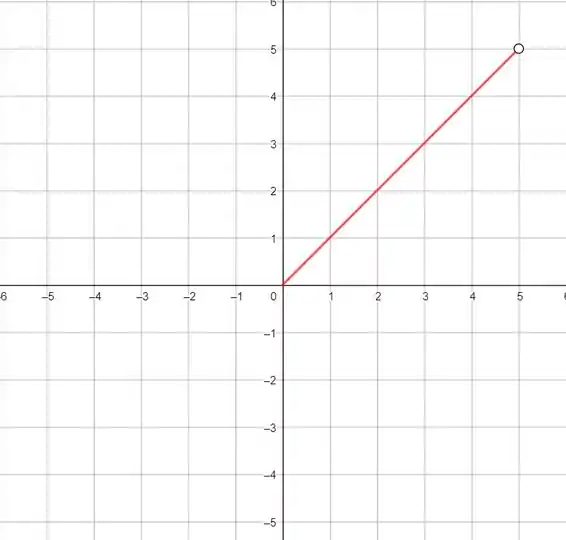
O próximo passo é espelhar isso que desenhamos do eixo , dessa forma:
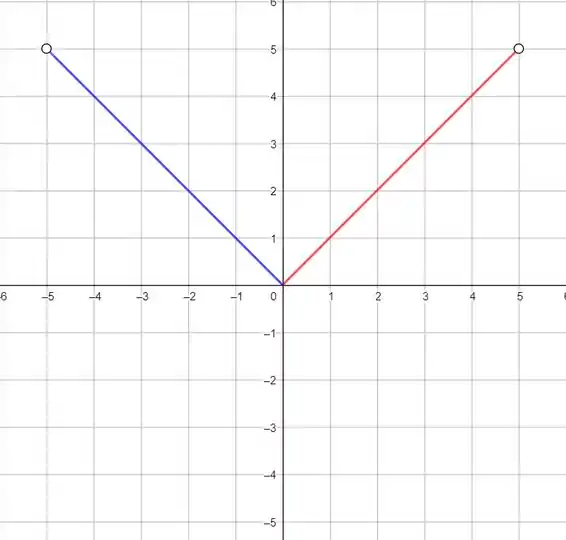
Cuidado com os pontos de descontinuidade! Temos que levar eles junto.
Beleza, mas isso ai seria uma extensão par, não é? Pra fazermos uma extensão ímpar temos que rebater essa parte azul no eixo , ou seja, jogar ela para baixo:
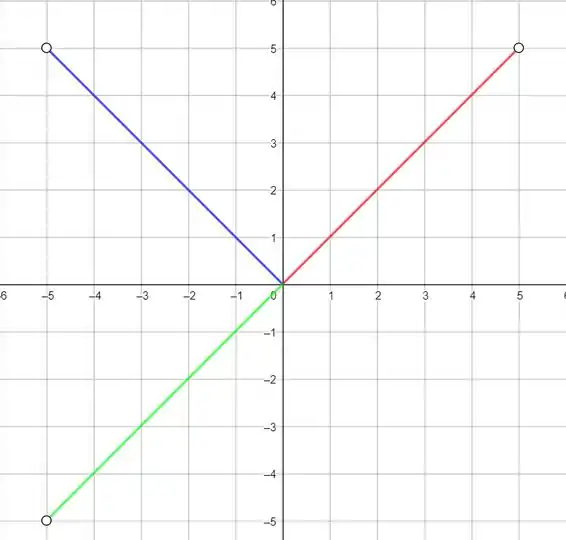
Certo, o período da função que queremos é então essa parte azul mais a vermelha! Como esse é o padrão que se repete, vamos copiá-lo para a direita, olha só:
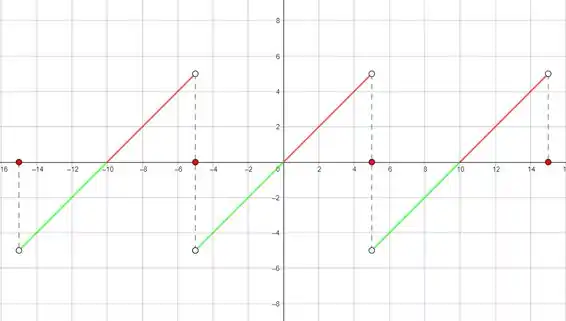
Pronto, temos então a função estendida no intervalo de a, como pede o enunciado. É bom você sempre desenhar esse tracejado grande para marcar o período da função, para não se perder!
Mais uma vez, lembre-se de levar os pontos de descontinuidade junto nesse passo a passo, ok?
Passo 2
Agora vamos fazer essa extensão matematicamente.
A definição de uma função ímpar diz que
Escrevemos porque estamos falando da extensão de , ok? Como a extensão tem período , podemos dizer que:
Beleza, vamos fazer isso aí. Como o período é , precisamos definir a função em e repetir esse padrão. Está faltando a definição de entre e .
Para :
Essa é a equação da parte vermelha.
Para :
Essa é a equação da parte verde. Se você se confundir com a definição de função ímpar, dá uma olhada no gráfico. Nesse caso, é até mais fácil.
Não podemos nos esquecer de que na origem e em a função deve valer zero em uma extensão ímpar, então está tudo certo aqui.
Temos portanto a seguinte extensão:
Como a função é periódica, isso se repete
Passo 3
Essa função tem período , logo . Então vamos calcular os coeficientes. Troque por se você achar mais conveniente para a série de senos! =)
Para resolver essa integral LINDA, vamos fazer integração por partes. Lembra?
O ideal nesse caso é a gente chamar de , então . Seguindo:
Passo 4
Como e :
E aí a série fica assim
Portanto:
Passo 5
Para resolver o problema por separação de variáveis, vamos escrever
Note que se trata de uma equação de calor.
Com a separação, teremos:
Portanto, nossa equação se torna
E isso origina duas equações (uma em e outra em ):
Passo 6
Agora, vamos olhar para as condições iniciais:
De e , se , então ambas as condições seriam atendidas. Mas como isso implicaria em , não atenderia à condição . Logo, .
Passo 7
Neste caso, nos resta admitir o seguinte:
Assim, formamos o seguinte problema:
Buscando uma solução não-trivial , vamos avaliar a equação característica:
E a solução geral é da forma
Passo 8
Aplicando as condições de contorno:
Note que na última equação não podemos ter (se não teríamos ). Então, precisamos de . Como , sobra
Passo 9
Como queremos , basta fazer , de modo que obtemos . Estes são nossos autovalores!
Portanto, ficamos com
que são nada mais nada menos que nossas autofunções!
Passo 10
Agora que já conhecemos os autovalores , vamos voltar pra equação em :
Fácil, né? Vamos substituir por :
E, assim, uma solução deve ser
Passo 11
Mas perceba só, se é solução, qualquer combinação linear de também será solução. Isto é, uma solução geral pode ser
Beleza, mas e agora, os coeficientes...? Bom, aí é só aplicar aquela condição , lembra?
Então, com :
Na letra , já achamos a série de Fourier da extensão ímpar de . Isso nos diz que esse é o coeficiente da série de Fourier que achamos lá na letra
E, finalmente, a solução é dada por