Uma barra de cobre de repousa em dois trilhos horizontais situados a de distância um do outro e é percorrida por uma corrente de . O coeficiente de atrito estático entre os trilhos é . Determine o módulo e o ângulo (em relação à vertical) do menor campo magnético que faz a barra se mover.
Passo 1
Beleza, esse não é dos mais fáceis, mas podemos dar conta numa boa...
Acontece que, como agora o campo magnético tem uma inclinação em relação à vertical, a força magnética sob a barra terá uma componente vertical e uma componente horizontal.
Antes de continuar, vamos definir como a componente horizontal do campo magnético e como a componente vertical do campo magnético, beleza? , por sua vez, é a força magnética gerada pelo campo magnético e , a força magnética gerada por .
Definindo o sentido da corrente indicado na figura, teremos a seguinte situação:
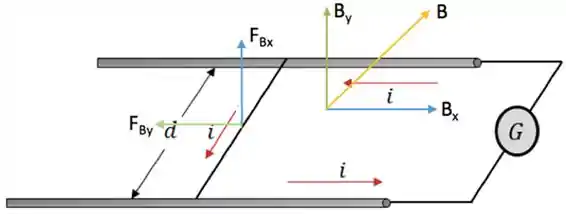
A menor força magnética na horizontal capaz de fazer o fio se mover deve ser igual à força de atrito estático. Logo:
Onde é o coeficiente de atrito estático e é a força normal.
Passo 2
A força normal é a reação entre a barra e os trilhos, logo:
Onde , portanto:
Passo 3
Fazendo o somatório de forças na horizontal, teremos:
Onde .
Como queremos descobrir o ângulo que o campo magnético faz com a vertical:
Jogando isso na equação de cima, teremos:
Reorganizando os termos, teremos o seguinte:
Beleza, mas o que faremos a partir daqui?
Passo 4
Para descobrir o ângulo em relação à vertical, vamos derivar a expressão de em relação e igualar o resultado a zero, beleza?
Dessa equação, , , , e são constantes, logo:
Para que essa razão seja nula, é necessário que o numerador seja nulo, portanto:
Onde :
Passo 5
Pra determinar o campo magnético, agora basta utilizar a relação de que encontramos no Passo 3.
Onde:
Jogando tudo em , teremos:
Resposta