A figura abaixo mostra um fio que conduz uma corrente . Ele é formado por dois trechos retilíneos de comprimento , ambos tangentes à mesma circunferência de raio , e por um arco desta circunferência que subentende um ângulo central de , conforme a figura abaixo.
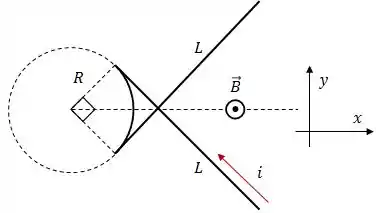
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano da página e orientado para fora dela.
Calcule o vetor força magnética que age sobre cada segmento de fio retilíneo;
Calcule o vetor força magnética que age sobre a parte circular;
Calcule a força resultante que age sobre o fio;
Passo 1
Calcule o vetor força magnética que age sobre cada segmento de fio retilíneo;
A força magnética sobre uma espira é dada por:
No caso de um fio retilíneo e campo magnético uniforme, podemos dar uma simplificada na fórmula:
Lembrando que é o vetor que aponta sempre na direção e sentido da corrente.
Aqui, vamos dividir o problema em duas partes... vamos resolver para o fio 1 e para o fio 3, como mostra a figura.
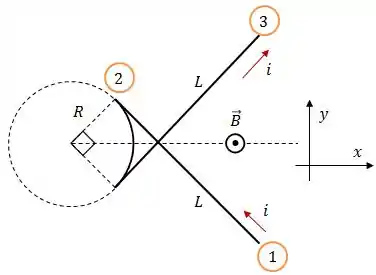
Passo 2
- Fio 1:
- Fio 3:
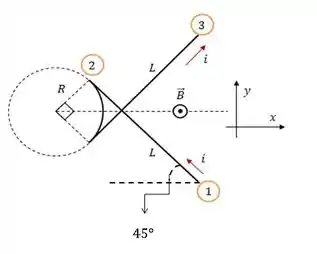
De acordo com o sentido que a corrente flui no fio 1, e sabendo que aquele ângulo vale podemos escrever como:
Como o campo magnético é dado por , teremos:
De acordo com o sentido que a corrente flui no fio 3, podemos escrever como:
Assim, a força magnética sobre o fio 3 será:
Passo 3
Calcule o vetor força magnética que age sobre a parte circular;
A ideia aqui é começar calculando a força sobre um elemento infinitesimal do fio circular, como mostra a figura:
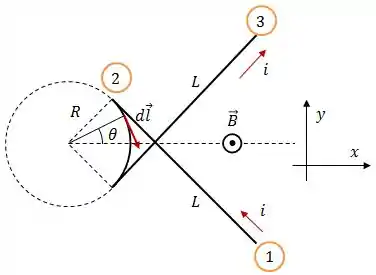
Logo:
Onde, de acordo com a figura acima:
Substituindo esses caras na expressão de , teremos:
Pra finalizar, temos apenas que integrar esse cara de até , seguindo o caminho da corrente, que vai de cima para baixo:
Onde:
Portanto:
Passo 4
Calcule a força resultante que age sobre o fio;
A força resultante no fio vai ser a soma vetorial das forças sobre os três fios, que nós já calculamos.
Agora é só organizar a bagunça:
Finalmente::
Resposta