Considere uma espira quadrada de lado percorrida por uma corrente . A espira se encontra no plano , conforme a figura.
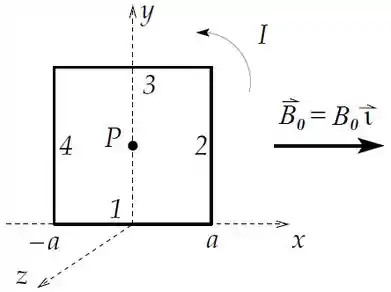
Calcule as forças resultantes e exercidas pelo campo externo sobre cada um dos lados do quadrado.
Passo 1
Calcule as forças resultantes e exercidas pelo campo externo sobre cada um dos lados do quadrado.
A força magnética sobre um condutor retilíneo, com o campo magnético uniforme, é dada por:
Onde aponta sempre no sentido da corrente.
Agora só temos que aplicar isso para cada fio.
- Fio 1:
- Fio 2:
- Fio 3:
- Fio 4:
No fio 1, a corrente vai da esquerda para a direita, logo:
Assim, a força sobre o fio 1 será:
No fio 2, a corrente vai de baixo para cima, logo:
Assim, a força sobre o fio 2 será:
No fio 3, a corrente vai da direita para a esquerda, logo:
Assim, a força sobre o fio 3 será:
No fio 4, a corrente vai de cima para baixo, logo:
Assim, a força sobre o fio 4 será:
Resposta