Três fios condutores finos, retilíneos e infinitos são alinhados paralelamente. Eles cruzam os vértices de um triângulo equilátero de lado , de forma que o plano deste triângulo é perpendicular aos eixos dos fios. A situação é mostrada na figura abaixo, onde os fios são designados por 1, 2 e 3. Ao medir-se a força magnética resultante por unidade de comprimento sobre o fio 1, obtém-se o vetor indicado na figura. Sabendo que os três fios são atravessados por correntes estacionárias, considere as afirmativas abaixo:
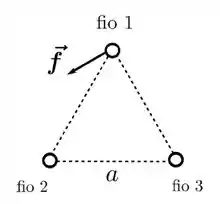
(I) As correntes que atravessam os fios 1 e 3 têm o mesmo sentido.
(II) As correntes que atravessam os fios 2 e 3 têm sentidos opostos.
(III) A corrente que atravessa o fio 2 tem intensidade maior que aquela que atravessa o fio 3.
São VERDADEIRAS as afirmativas:
(a) Apenas II e III
(b) Apenas I
(c) Apenas II
(d) Apenas III
(e) Apenas I e II
(f) Apenas I e III
(g) I, II e III
(h) Nenhuma delas
Passo 1
Vamos lá!
O vetor é o vetor força resultante sobre o fio , isso quer dizer que:
Vamos analisar cada uma separadamente.
A força que o fio 3 faz no fio 1 é:
Então para descobrirmos a força que 3 faz em 1, precisamos saber qual o campo magnético do fio 3 na posição do fio 1.
O campo magnético de um fio infinito é dado por:
Como o exercício é mais qualitativo (não pede valores de nada) não vamos fazer as contas em si, vamos só analisar os sinais e tudo mais.. Então vamos lá!
As possíveis direções e sentidos do campo magnético gerado por 3 na posição do fio 1 são:
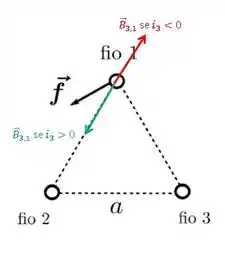
Já que o vetor não muda, o que tá influenciando é justamente a orientação da corrente, ou seja, o vetor . Na figura, eu mostrei os dois campos possíveis, de acordo com o sentido da corrente: se quer dizer que está fluindo no sentido positivo do eixo z. e se quer dizer que está fluindo no sentido negativo do eixo z.
Agora que já sabemos os possíveis campos de 3 em 1, vamos analisar as possíveis forças que 3 faz em 1.
Já vimos que:
Então vamos analisar os possíveis resultados desse produto vetorial, que depende do sentido da corrente em 1 e do campo magnético do fio 3, que por sua vez, depende do sentido da corrente .
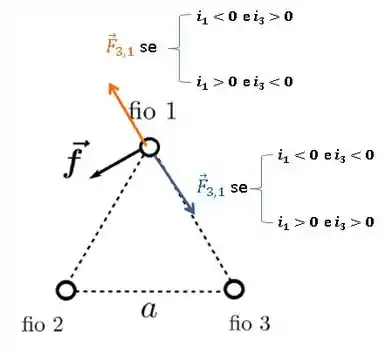
Beleza! Já temos as possíveis forças que o 3 faz em 1. Vamos fazer a mesma coisa para o fio 2.
Passo 2
As possíveis direções e sentidos do campo magnético gerado pelo fio 2 na posição do fio 1 são:
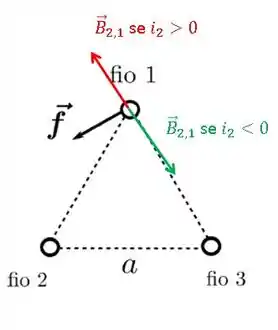
E com isso, as possíveis forças em 1 geradas por 2 são:
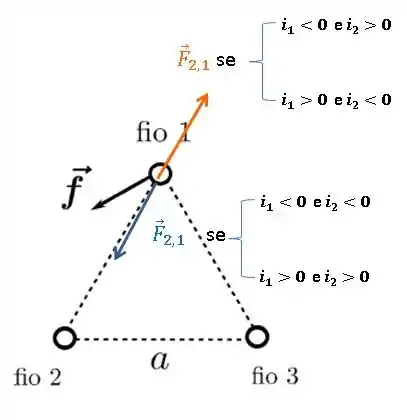
Show de bola!
Passo 3
Lembrando que a força resultante tem essa forma:
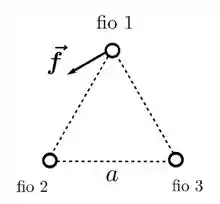
Então a pergunta é: qual das possíveis forças que nós achamos podem resultar nesse vetor aí de cima?
A resposta é: o vetor força de 2 para baixo e o vetor força de 3 para cima:
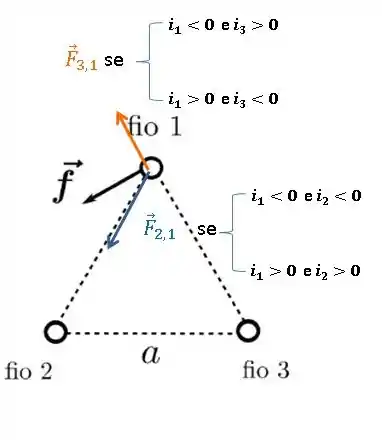
E com isso, já temos os sentidos das correntes ali. Então vamos analisar as afirmativas.
Passo 4
- As correntes que atravessam os fios 1 e 3 têm o mesmo sentido.
- As correntes que atravessam os fios 2 e 3 têm sentidos opostos.
Lá n figura, a gente viu que ambas as possibilidades mostram que as correntes de 1 e de 3 estão opostas. Então essa é falsa.
Para temos as seguintes possibilades: e . Para temos as possibilidades: e Ou seja, em ambos os casos e são opostas. Logo essa afirmativa é verdadeira.
(III) A corrente que atravessa o fio 2 tem intensidade maior que aquela que atravessa o fio 3.
Podemos olhar para a figura e ver que o vetor está mais para “baixo”, ou seja, a força que puxa para baixo é mais intensa. E essa força é a força 2. Logo essa está certa também.
Resposta
a