UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 3b,c
Uma fita metálica de largura conduz uma corrente . Portanto, a densidade superficial de corrente é
- Se tivermos uma partícula de carga , positiva, com velocidade se movendo em uma direção ortogonal ao plano da fita, se aproximando da fita e muito próxima a ela, qual será o módulo da força magnética que age sobre a partícula?
- Descreva o sentido da força do item (b)
Passo 1
Oi, tudo bem?
Letra b) e c)
No item (a) foi pedido o campo magnético nos pontos próximos à superfície da fita. O caminho que escolhi para aplicar a lei de Ampére foi esse aqui
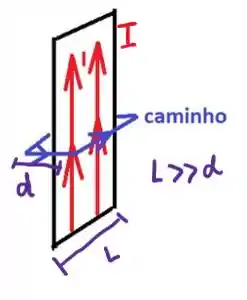
E agora o problema pede para calcular o módulo da força magnética de uma partícula positiva que entra na fita. O módulo da força magnética é dado por
Onde é o ângulo entre a velocidade e o campo.
Consideramos a corrente vertical para cima, e aplicamos a lei de ampère. Sendo assim, o campo vai estar ao longo da direção do caminho escolhido, ok?
E considerando que o campo está ao longo de , então o campo está na direção , como o desenho.
Então vemos que se a partícula entrar na fita metálica, ela entra perpendicular ao campo. Então
E daí
E a força magnética
O módulo do campo que encontramos é , então vamos utilizar aqui!
Passo 2
Agora é só substituir os valores!
A forma será
Beleza?
Passo 3
E agora a direção dessa força!
Para determinar a direção, vamos relembrar qual é a fórmula vetorial da força magnética
Como já sabemos o módulo, só nos resta determinar a direção e o sentido! Então o que vamos fazer é identificar o vetor de e de , e fazer o produto vetorial entre eles!
A partícula entra perpendicular à superfície da fita, como a fita está ao longo do eixo , então o sentido da velocidade é
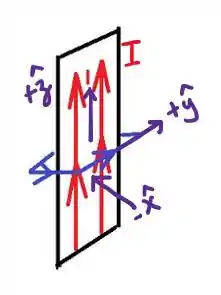
Sendo assim, a direção e o sentido da força são: vertical para cima.
Tranquilo? Espero ter ajudado!