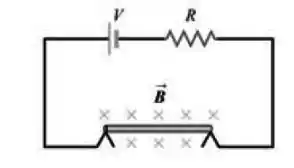
Uma barra metálica delgada, com de comprimento e massa , repousa sobre dois suportes metálicos (mas não está conectada a eles), em um campo magnético uniforme de , como indica a Figura abaixo. Uma bateria com ddp e um resistor de em série estão conectados aos suportes.
- Qual voltagem máxima a bateria pode ter sem romper o circuito nos suportes?
- A voltagem da bateria possui o valor máximo calculado no item (a). Supondo que o resistor repentinamente sofre um curto-circuito parcial, diminuindo sua resistência para , ache a aceleração inicial da barra.
Passo 1
a) Aqui temos um típico problema de força em um condutor pelo qual passa corrente e que está na presença de um campo magnético. Quando esse condutor é percorrido por um corrente, ele sofre uma força que tem módulo dado
Bom, essa força precisa estar direcionada para cima para poder equilibrar o peso da barra. Portanto, o sentido da corrente deve ser anti-horário na Figura acima. Se a gente igual a força peso com a força magnética, chegamos a
Se uma corrente maior do que esse valor passar pela barra, então, a barra vai sentir uma força maior do que a força peso e vai ser acelerada para cima, que o caso que a gente vai ver no próximo item.
Continuando aqui, por enquanto, e colocando os valores dados no enunciado, o valor dessa corrente é
Então, a diferença de potencial é dada por
Passo 2
b) Se a ddp é a mesma que no caso do item (a), então a corrente agora vai ter o seguinte valor
que é bem maior do que a do caso anterior. Isso significa que a barra vai sofrer uma nova força magnética para cima maior do que o seu peso e, por isso, vai ser acelerada para cima. A aceleração que ele vai ter é
Colocando os valores da nova corrente e os do enunciado, a barra tem uma aceleração que é dada por