O fio dobrado da figura abaixo está submetido a um campo magnético uniforme. Cada trecho retilíneo tem de comprimento e faz um ângulo de com o eixo .
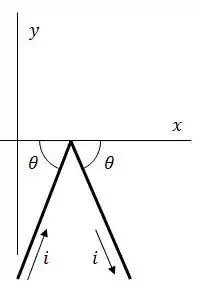
O fio é percorrido por uma corrente de . Qual é a força que o campo magnético exerce sobre o fio em termos de vetores unitários, se o campo magnético é:
;
;
Passo 1
;
Como os trechos retilíneos tem o mesmo comprimento, é uma boa tentarmos explorar a simetria do problema.
A força magnética sobre um fio retilíneo é dada por:
Aplicando a regra da mão direita, teremos o seguinte:

Analisando as forças, podemos perceber que as suas componentes na direção se anulam e as componentes na direção se somam.
A componente em sobre o primeiro fio será:
Logo:
Assim, a força resultante será:
Além disso, podemos ver que a força resultante estará apontando no sentido .
Passo 2
;
Novamente, partindo da regra da mão direita, podemos ver que, em ambos os fios, a força magnética estará apontando na direção , como mostra a figura abaixo.
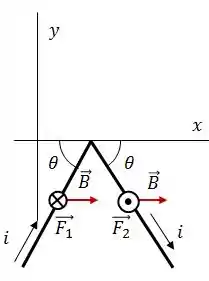
Como os dois fios são tem o mesmo tamanho, não é difícil concluir que .
Logo, as duas forças irão se anular e a força resultante total será nula:
Resposta