Forças e Torque sobre uma Espira
Calcule a força magnética resultante sobre o pedaço de fio, através do qual passa uma corrente elétrica estacionária de intensidade , composto por dois segmentos retilíneos, de comprimento , muito grande, e uma semicircunferência de círculo, de raio , na presença de um campo magnético constante (estacionário e uniforme) , .
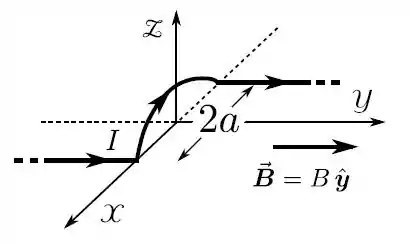
Passo 1
A força magnética é dada por:
No caso de uma distribuição contínua de cargas em movimento (corrente), utilizamos a expressão equivalente:
E integramos no circuito todo:
Basta determinarmos o sentido do produto vetorial para cada segmento. Podemos mostrar que para os retilíneos não há força por conta do produto nulo:
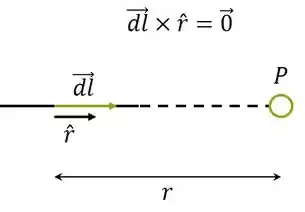
O que é conveniente, senão teríamos que fazer uma integral com limites de integração infinitos.
Passo 2
Fazendo agora o produto para o segmento semicircular:
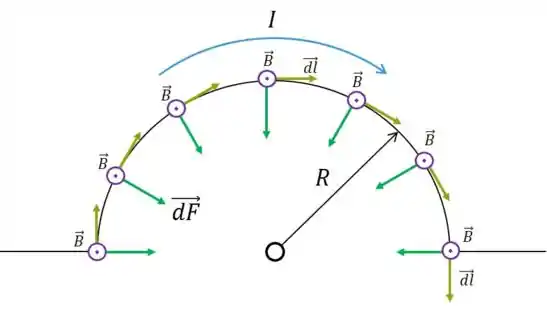
Podemos ver que sempre aponta para o centro, o que é uma pena. Nosso produto vetorial admite variabilidade, então não podemos tirar ele fora da integral... Por simetria sabemos que não vai haver componente no sentido de , como as respostas das múltiplas escolhas já sugerem.
Passo 3
Vamos decompor o vetor e achar a componente dela em :
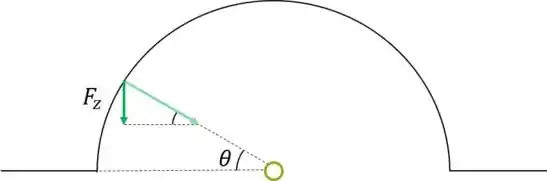
Calculando o módulo dele:
Trocamos para coordenadas polares:
Passo 4
Que resulta em:
Ajustamos o vetor para apontar pra baixo (pois já sabemos a orientação):
Resposta
Letra b