Duas partículas de cargas e são fixadas sobre o eixo de um sistema de coordenadas nos pontos e , respectivamente (). Em que ponto desse eixo deve ser posicionado uma terceira partícula de carga de forma que ela fique em equilíbrio?
Passo 1
Bem... Infelizmente o problema não nos trouxe um desenho do que está acontecendo, então acho melhor a gente começar por aqui, pode ser?
Temos duas cargas e posicionadas nos pontos e ...
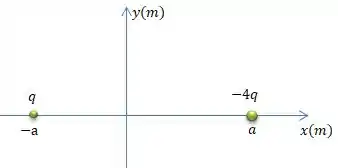
E aí, nós vamos inserir uma terceira carga de modo que essa terceira carga fique em equilíbrio (ou seja, não haja forças elétricas atuando sobre ela). Para que isso ocorra, de acordo com a nossa teoria, essa terceira carga deve ser posicionada na posição que o campo elétrico formado por essas duas cargas verdes seja ...
Então é isso que vamos procurar, ou seja, o ponto onde o campo elétrico seja nulo! Vamos nessa?
Passo 2
POW! O campo elétrico de duas cargas pontuais pode ser dado pela Lei de Coulomb...
Onde é a carga , e é a segunda carga. e , por sua vez representam a distância das cargas e ao ponto que queremos calcular o campo elétrico nulo. No nosso caso...
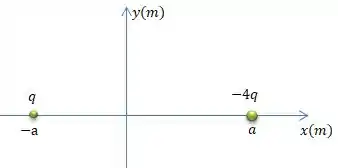
Podemos escolher e e , de modo que o campo elétrico em todo o espaço feito por essas duas partículas é...
POW! Mas sabia que podemos escrever em função de ?
Passo 3
POXA! Não sabemos onde teremos que colocar a terceira partícula, mas podemos ter uma leve noção onde isso vai acontecer!
Por simetria, a terceira partícula só poderá estar localizada no eixo . E provavelmente próximo da carga , afinal essa carga vai repelir, enquanto que a vai atrair fazendo com que essa terceira carga se equilibre, saca?
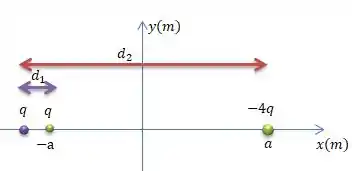
Então repare que podemos falar que...
Passo 4
Jogando esse resultado na fórmula do campo elétrico...
E sabendo que o ponto onde a terceira carga se encontra deve ter campo elétrico nulo...
Reorganizando...
Resolvendo esse lado direito...
Resolvendo essa equação para usando Báskara...
Então...
Como não pode ser negativo por se tratar de uma distância...
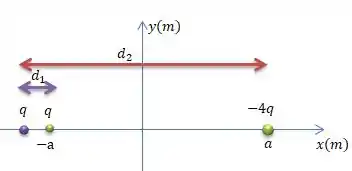
Concluímos que , e, portanto, a posição da carga azul vai ser , saca?
Resposta
Letra A