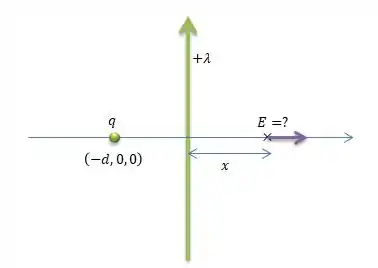
Parte 1: Um fio isolante infinito, alinhado com o eixo , está carregado com a densidade de carga positiva . Uma carga pontual, com valor , é colocada no ponto , sendo .
a) Calcule o campo elétrico nos pontos , sendo .
b) Encontre o valor de no qual o campo elétrico é nulo.
Parte 2: Três cargas pontuais idênticas estão situadas nos vértices de um triângulo equilátero de lado .
c) Calcule a energia eletrostática do sistema.
d) Calcule a que distância das cargas está o ponto no qual o campo elétrico é nulo.
Passo 1
PARTE 1:
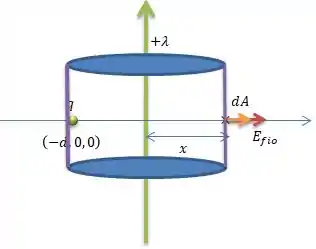
Bem... Como não temos o desenho dessa configuração de cargas dessa parte , acho melhor começarmos por um desenho, pode ser?
No problema temos duas fontes de carga: um fio com densidade de carga no eixo e uma carga pontual ...
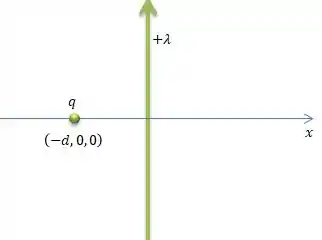
E na letra , ele pede para encontrarmos o campo elétrico desse conjunto de cargas em um ponto no eixo a uma distância do fio...
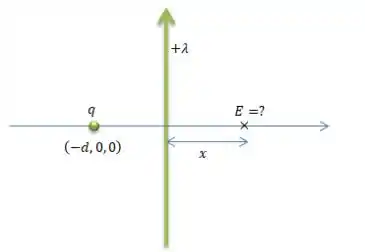
Beleza! E aí? Como proceder?
Bem... Temos duas fontes de campo elétrico: o fio e a carga, então...
Então é só calcularmos o campo elétrico de cada separado e depois somarmos! Vamos nessa?
Passo 2
Primeiro vamos encontrar o campo elétrico da carga que é mais tranquila!
A teoria nos diz que o campo elétrico de uma carga elétrica pontual é dado pela Lei de Coulomb...
Onde é a distância entre a carga e o ponto onde estamos medindo o campo elétrico. POW! No nosso caso, a distância entre a carga e o ponto do campo é , então...
Passo 3
Agora vamos para o campo produzido por uma reta de carga, beleza?
Para isso, vamos usar a Lei de Gauss que nos diz que o fluxo do campo elétrico dentro de uma Gaussiana deve ser igual á...
Onde é a Gaussiana, uma superfície fechada que devemos construir ao redor do fio. No Caso, a Gaussiana mais adequada tem que ser um cilindro de raio ...
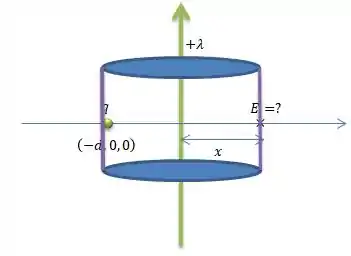
Então a carga presa dentro do cilindro produz um campo elétrico que é radial ao fio sempre...
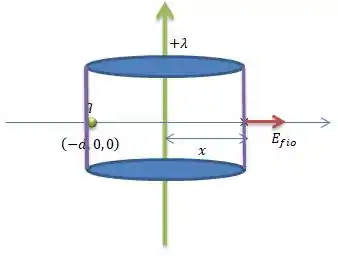
E olha que maneiro cara, o campo elétrico é perpendicular a superfície do cilindro, o que é o mesmo que dizer que o campo elétrico do fio então tem a mesma direção que o vetor de área da superfície do cilindro...
Pela álgebra, se tivermos dois vetores na mesma direção o produto vetorial deles será apenas o produto dos módulos (tamanhos). Sendo assim, podemos dizer que o produto escalar entre os vetores é igual ao produto dos módulos, isto é...
Então...
Como o campo elétrico é constante ao longo de todo o cilindro (Gaussiana)...
E agora quem é a integral de ? Isso mesmo! É a área da Lateral do cilindro!
Onde é o raio do cilindro e é a altura do cilindro...
Agora, o que significa ? SIM! É a densidade de carga do fio...
Viu só! A Lei de Gauss é maravilhosa mesmo, neh? MAS ATENÇÃO: a integral de superfície deve ser sempre calculada em uma superfície fechada. E a partir da , nós trocamos a integral de superfície fechada para uma integral na lateral do cilindro apenas, já que o fluxo de campo elétrico nas tampas do cilindro é (afinal o campo elétrico não sai e nem entra a partir das tampas, ta ligado?
Passo 4
Então, concluindo a Letra A, podemos dizer que o campo elétrico no eixo é...
E ainda em termos de vetor, podemos dizer que esse campo no eixo aponta na direção do eixo ...
Ou seja...
Passo 5
Nesse item apenas temos que encontrar o ponto onde o campo elétrico se anula. Para isso...
Então...
Logo...
Resolvendo esse quadrado do lado esquerdo...
Repare ainda que podemos escrever esse lado esquerdo como...
Ou seja...
Então essa é a distância onde o campo elétrico é nulo .
Passo 6
PARTE 2:
Assim como no início do exercício , vamos desenhar primeiro essa configuração de cargas, pode ser?
Temos três cargas pontuais de cargas dispostas em um triângulo equilátero de lado ...
Passo 7
POW! Pela teoria sabemos que energia eletrostática pode ser dada por...
Onde e é o par de cargas e é a distância entre elas!
Então, no nosso caso temos três pares...
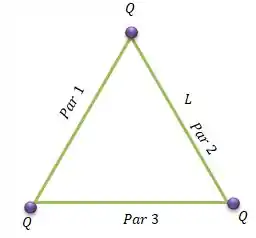
Para cada Par desse aí a energia eletrostática será...
Logo, a energia eletrostática total será...
Passo 8
POXA! Se temos três cargas pontuais idênticas, o ponto onde teremos campo elétrico será nulo será no centro geométrico da figura...
De acordo com a nossa linda Geometria, o centro de um triângulo equilátero (baricentro) acontece a da altura ...
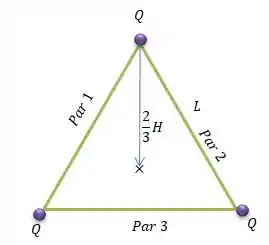
E a altura é dada por Pitágoras...
Então a distância de cada carga ao ponto de campo elétrico nulo será...
Resposta
Letra A:
Letra B:
Letra C:
Letra D: