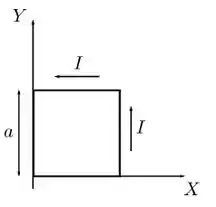
Uma espira condutora quadrada de lado é posicionada sobre o plano de um sistema de coordenadas como mostrado na figura abaixo. Seus lados são paralelos aos eixos e um de seus vértices está sobre a origem. Ela transporta uma corrente estacionária de intensidade e sentido anti-horário e está imersa em uma região de campo magnético estacionário, mas não-uniforme dado por, onde é uma constante positiva. Sobre essa situação, é CORRETO afirmar que a força magnética resultante sobre a espira:
(a) Aponta no sentido
(b) Aponta no sentido
(c) Aponta no sentido
(d) Aponta no sentido
(e) Aponta no sentido
(f) Aponta no sentido
(g) É nula.
Passo 1
A força magnética em cada região da espira vai ser dada por
Vamos dividir as regiões da espira assim:
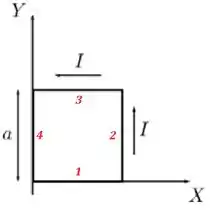
Então a gente calcula em cada uma das regiões e depois soma todas pra encontrarmos a direção da força resultante :)
Passo 2
Vamos calcular para a região 1:
Fazendo o produto vetorial:
Passo 3
Para a região 2:
Nesse caso, é fixo, portanto , logo, a resolução dessa integral é dada por
Passo 4
Na região 3:
Passo 5
Na região 4:
Nesse caso, o também é fixo, mas , logo:
Passo 6
A força resultante será
Logo, a força magnética está na direção e portanto a alternativa correta é a letra A :D
Resposta
(a) Aponta no sentido