Na figura abaixo, um fio metálico de massa pode deslizar com atrito insignificante sobre dois trilhos paralelos horizontais separados por uma distância .
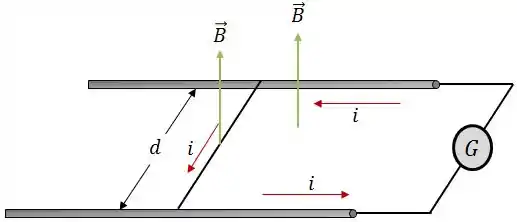
O conjunto está em uma região onde existe um campo magnético uniforme de módulo .
No instante um gerador é ligado aos trilhos e produz uma corrente constante no fio e nos trilhos (mesmo quando o fio está se movendo). No instante , determine:
a velocidade escalar do fio;
o sentido do movimento do fio (para a esquerda ou para a direita).
Passo 1
Determine a velocidade escalar do fio;
Sabendo que a força resultante sobre o fio deslizante é a força magnética, podemos dizer, a partir da segunda lei de Newton, que:
Logo, a aceleração da barra será dada por:
Como a corrente é constante, a aceleração também será constante. Portanto:
Como a velocidade inicial do fio é nula, teremos:
Onde:
Jogando isso tudo na expressão da velocidade, teremos:
Passo 2
Determine o sentido do movimento do fio (para a esquerda ou para a direita).
O sentido do movimento será dado pelo sentido da força magnética. Aplicando a regra da mão direita, teremos:
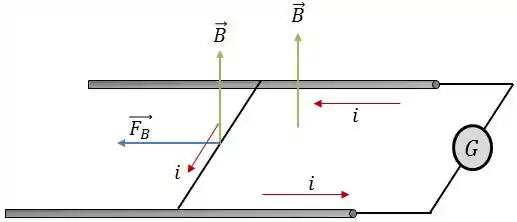
Logo, o fio se movimentará para a esquerda.
Resposta
O fio se movimentará para a esquerda.