A figura abaixo mostra três fios que conduzem correntes da mesma intensidade do ponto ao . O fio é formado por dois segmentos de reta inclinados de mesmo comprimento, o fio é um único segmento de reta horizontal de comprimento e o fio é um semicírculo de diâmetro . O segmento de reta tracejado na figura tem comprimento . Os fios estão numa região de campo magnético constante perpendicular ao plano da página, com sentido para dentro. Sejam , e as intensidades das forças magnéticas que o campo exerce sobre os fios , e respectivamente. Nessas condições, podemos afirmar que:
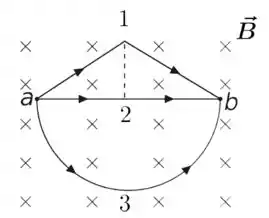
Passo 1
A primeira coisa de que precisamos nos lembrar aqui é que a força magnética que atua sobre um condutor pelo qual passa uma corrente é dada por
onde é um elemento infinitesimal do comprimento do condutor que tem a mesma direção e sentido da corrente que passa por ele, é o campo magnético na região onde está esse condutor e a integral é feita sobre toda o comprimento do condutor.
Como o problema diz para a gente que o campo magnético é uniforme, então sobre toda a extensão de cada um dos fios esse campo tem o mesmo valor. Por isso, para cada um dos fios, podemos tirar da integral na expressão para acima e escrever que
O que precisamos fazer agora é calcular o valor da integral para cada um dos fios da Figura acima. Dado o sistema de referência, a “receita de bolo” será a seguinte:
i) primeiro, encontramos o vetor ;
ii) integramos sobre o comprimento dos condutores.
Agora, mãos à obra....
Passo 2
FIO 1: Nesse caso, como mostra a Figura abaixo, a direção e sentido do elemento em cada uma das metades desse fio são sempre os mesmos e, por isso, a força em cada uma das metades do fio 1 terá o mesmo módulo, com as direções e sentidos constantes ao longo de cada metade. Esses vetores são desenhados na Figura abaixo.
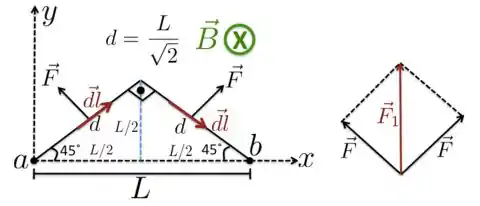
Na primeira metade do fio 1, o vetor será escrito como
Quando integrarmos esse vetor, teremos
Então, a força na primeira metade do fio 1 será
De maneira análoga, o vetor na segunda metade do fio é
que nos permite encontrar a força na segunda metade do fio 1, que será
Então, para a gente saber qual será a força resultante total sobre o fio 1, basta somarmos, vetorialmente, os vetores em cada uma das metadesIsso nos dá que
Esse vetor resultante está desenhado à direita da Figura acima em vermelho.
Passo 3
FIO 2: Nesse caso, a força ao longo de todo o fio terá o mesmo módulo e estará na mesma direção e sentido, como mostra a figura abaixo.
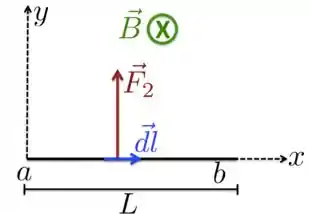
Nesse caso, como , então
Portanto, a força será igual a
Como , a força é
Passo 4
FIO 3: Para vermos como fica o vetor nesse caso, vamos redesenhar o fio 3 como na Figura abaixo.
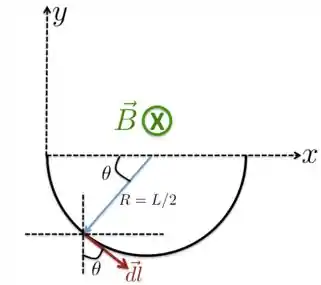
Nesse caso, como o raio desse semicírculo é , temos
Portanto, a integral é
pois a segunda integral depois da primeira igualdade é nula. Simplificando a expressão acima, temos
A força nesse caso vai ser dada por
Portanto, as intensidades das forças , e são iguais.
Resposta
Letra c).