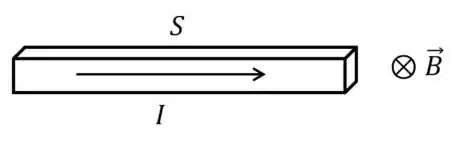
A figura mostra um condutor com uma corrente que flui da esquerda para a direita, imerso em um campo magnético dirigido para “dentro” da página. A superfície (superior) está a um potencial maior que a superfície (inferior). Os portadores de carga:
a) são negativos
b) são positivos
c) são neutros
d) são ausentes
e) movem-se com velocidade próxima à da luz
Passo 1
O enunciado diz que “a superfície superior está a um potencial maior que a superfície ”. O que isso quer dizer?
Vamos ver como esse potencial se relaciona com o campo elétrico:
O gradiente aponta na direção e sentido em que o potencial aumenta.
Ou seja, se o potencial é maior na superfície de cima do condutor, o gradiente vai apontar para cima.
Mas já que temos aquele sinal de menos ali, isso vai ser invertido e então o campo elétrico aponta para a superfície de baixo do condutor:
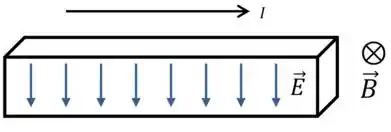
Beleza, então a gente sabe que existe um campo elétrico dentro do condutor, apontando para baixo.
Passo 2
Então tá, de onde está vindo aquele campo? Alguma coisa tem que estar empurrando as cargas positivas para cima e as negativas para baixo, só assim teríamos um campo daquele jeito.
É aí que entra aquele campo magnético externo . O que acontece quando uma corrente fica imersa em um campo magnético? Sofre uma força.
Inclusive talvez você já tenha visto esse fenômeno antes: é o efeito Hall!
Cada uma das cargas que formam a corrente vai estar sujeita a essa força aqui:
No nosso caso, aponta na direção e sentido da corrente, e aponta para dentro da página.
Vamos usar a regra da mão direita pra descobrir a direção da força nesse caso:
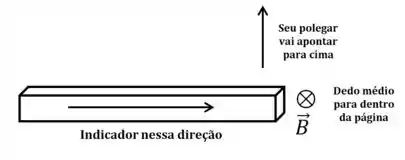
A direção onde seu polegar aponta é a direção da força magnética sobre as cargas.
Passo 3
Ok, e o que isso tudo tem a ver com o sinal das cargas? Vamos ver duas hipóteses.
1) Bom, se as cargas são positivas, então a velocidade aponta na mesma direção da corrente: . Além disso, .
Então o sinal da força vai ser o mesmo daquele que colocamos no desenho, e as cargas positivas serão empurradas para cima.
2) Se as cargas são negativas, então a velocidade das cargas é contrária à corrente (), e além disso .
Nesse caso, o sinal das forças também vai ser o mesmo (os dois sinais negativos se cancelam!), e então as cargas negativas também seriam empurradas para cima.
Mas a gente viu lá em cima que, pra explicar o potencial que a questão mencionou, temos que ter cargas positivas acumuladas na parte de cima do condutor.
Isso quer dizer que as nossa corrente é composta de portadores de carga positivos: a primeira hipótese deu certo, a segunda não.
Resposta
Letra (b).