Um fio fino, transportando uma corrente , é dobrado na forma de um grampo composto por dois segmentos retilíneos de comprimento e um arco semicircular de raio .
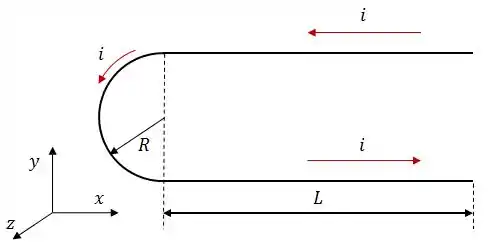
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano do fio e orientado para fora da página, conforme figura ao lado.
- Calcule o vetor força magnética que age sobre cada fio retilíneo;
- Calcule o vetor força magnética que age sobre a parte circular;
- Calcule a força resultante que age sobre o fio todo;
Passo 1
- Calcule o vetor força magnética que age sobre cada fio retilíneo;
Beleza! Pra começar, vamos dividir esse cara em três partes, as duas retilíneas e a semicircular.
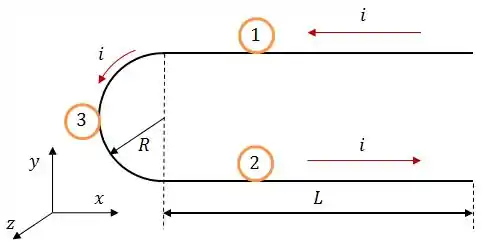
A força magnética sobre um fio é dada por:
Onde o segmento aponta sempre na direção da corrente.
Nesses casos, como se tratam de fios retilíneos:
- Fio 1:
- Fio 2:
Logo:
Portanto:
Passo 2
Pra termos uma ideia de pra onde está apontando vamos pegar um ponto aleatório do fio semicircular:
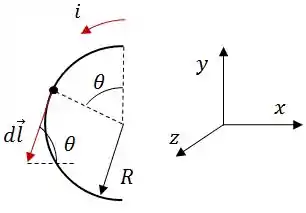
Podemos decompor o vetor nos eixos ortogonais como:
Como é o elemento infinitesimal desse arco, podemos escrevê-lo como:
Agora podemos calcular a força:
Passo 3
A força resultante será a soma vetorial das forças que já calculamos, logo:
Resposta
a.
b.
c.