. Um fio condutor fino, retilíneo e infinito é posicionado sobre o eixo de um sistema de coordenadas. Um segundo fio condutor fino, retilíneo e finito, de comprimento , é posicionado sobre o eixo com sua extremidade mais próxima a uma distância do primeiro fio, como mostrado na figura abaixo. Os fios transportam correntes estacionárias de intensidades e nos sentidos indicados. Quais são o módulo e o sentido da força magnética resultante que o primeiro fio exerce sobre o segundo?
Dados:
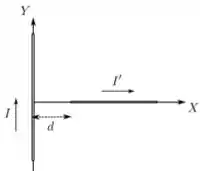
Escolha uma opção:
positivo
negativo
negativo
negativo
positivo
positivo
negativo
positivo
Passo 1
Vem comigo que a gente resolve essa juntos!
Para encontrar a força que o fio infinito faz sobre o fio finito, vamos usar a equação de uma força magnética sobre um fio, que é dada por:
Onde é o módulo do campo que passa por esse fio, é a corrente que atravessa o fio que estamos interessados e é o ângulo entre a direção do campo e a direção da corrente .
O campo que atua no fio finito é o gerado pelo infinito que é dado por:
Onde é a corrente que passa pelo fio que gera o campo e é a distância entre o fio e onde estamos interessados de saber o valor do campo.
Usando a regar da mão direita vemos que o campo gerado pelo fio infinito aponta para dentro da página, vamos chamar essa direção de . Então:
Vamos seguindo!
Passo 2
O vetor aponta na direção da corrente que passa pelo fio finito, assim , então temos o seguinte:
O produto vetorial ,assim:
Passo 3
Agora vamos integrar os dois lados da expressão que chegamos, o lado direito vamos integrar de até que vai dar o comprimento do fio finito, assim:
Onde fizemos só para o nome das variáveis baterem, asism:
Substituindo os valores que temos, ficamos com:
Com isso temos que:
Então nossa alternativa correta é a letra .
Resposta
positivo