Halliday - Vol. 3 – 9º edição – Capítulo 28 – Seção 8 – Exercício 47
(Capítulo 28.8 – Exercício 47) Uma barra de cobre de 1,0 kg repousa em dois trilhos horizontais situados a 1,0 m de distância um do outro e é percorrida por uma corrente de 50 A. O coeficiente de atrito estático entre a barra e trilhos é 0,60. Determine (a) o módulo e (b) o ângulo (em relação à vertical) do menor campo magnético que faz a barra se mover.
Passo 1
Faala pessoal! Vamos desenhar o que está acontecendo com uma vista de cima, supondo um sentido para a corrente:
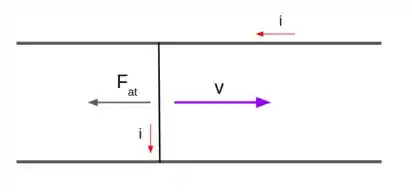
Sabemos que a força magnética é calculada por
Dessa forma a força na vertical é:
E para a parte horizontal temos:
E aí queremos encontrar o momento em que a barra sai da inércia, vamos lá!
Passo 2
a) Como queremos saber o momento em que a barra sai da inercia:
Agora, vamos escrever cada componente do campo magnético em relação ao módulo do vetor. O vetor campo magnético tem módulo , portanto, , , assim:
Colocando o campo em evidência:
Agora precisamos achar o ponto de mínimo
Passo 3
Para achamos o ponto de mínimo, vamos derivar a equação por e igualar a zero:
Portanto,
Passo 4
(b) Como visto no item (a)
Sucesso!
Resposta
(a)(b)