Na figura abaixo o campo magnético é uniforme e perpendicular ao plano da figura, apontando para fora (direção positiva do eixo ). A espira é formada por um quarto de círculo de raio (arco ) e por dois segmentos retilíneos e de comprimento , conforme-te a figura. Pela espira circula uma corrente no sentido anti-horário.
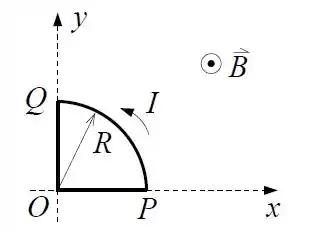
Calcule a força magnética em cada um dos três trechos , e da espira.
Passo 1
Calcule a força magnética em cada um dos três trechos , e da espira.
Beleza! Vamos começar pelos fios retilíneos, tranquilo?
A força magnética sobre um fio condutor é dada por:
Como aqui trata-se de corpos retilíneos, e tanto a corrente quanto o campo magnético são constantes, podemos simplificar a fórmula para:
Obs: Uma coisa que você não pode esquecer é que o vetor aponta sempre na direção e sentido da corrente.
Passo 2
- Fio vertical:
- Fio horizontal:
- Fio circular:
No fio vertical, a corrente flui de cima para baixo, logo, podemos dizer que:
Assim, a força magnética será:
Nesse fio, a corrente flui da esquerda para direita, então podemos dizer que:
E a força magnética será:
Ok! Aqui tem duas formas de resolver esse problema... se você pode tentar pegar um pedaço infinitesimal do fio, escrever o vetor para ele e resolver a integral:
Acredite em mim, vai dar certo! Tem que dar certo!
Oooooooou você pode guardar, nesse momento singular, uma coisa que vai ser muito útil e vai te economizar um tempo ABSURDO!
Quando o campo magnético é uniforme, a força magnética sobre uma espira é ZERO!
Opaaa! Sabe o que isso quer dizer?! Sim, é exatamente isso que você está pensando...
Se a força magnética resultante sobre a espira é zero, para sabermos a força magnética sobre o fio circular, basta fazer:
Resposta