Uma espira retangular de lados e é colocada em duas regiões: a superior com campo magnético e a inferior com como mostra a figura ao lado. A espira é percorrida por uma corrente de intensidade no sentido apresentado na figura.
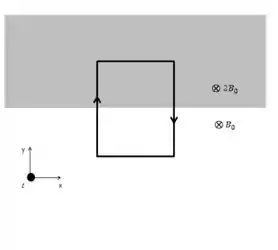
a) Qual deve ser a massa da espira (preste atenção no sentido da gravidade na figura) para que ela fique suspensa no ar?
b) Qual deve ser o novo valor da massa para que a espira permaneça em equilíbrio quando mudamos sua orientação para a mostrada na figura inferior?
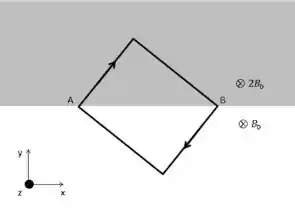
Passo 1
a)
Aqui temos uma espira que está sujeita a dois campos magnéticos. Se ela cair, ela vai descer no eixo y, então a gravidade está nessa direção. Como queremos saber a massa da espira para que ela não caia, temos que as forças na direção y devem satisfazer
E quais serão essas forças? Serão as forças magnéticas, devido aos campos,e a própria força peso da espira.
Na parte da espira superior, teremos a força:
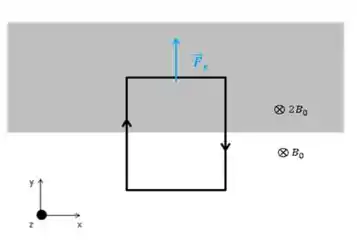
Pela regra da mão direita, como a corrente vai para a direita e o campo entra em z, temos que a força é positiva em y.
Substituindo os valores:
Já a força na parte inferior da espira está relacionada ao campo mais fraco
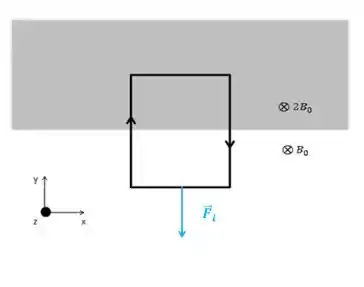
Como a corrente, nessa parte da espira vai para a esquerda, horizontalmente, e o campo entra em z, temos que, pela regra da mão direita, a força magnética estará na direção y, no sentido negativo.
Substituindo os valores:
Então na direção vertical, temos essas duas forças magnéticas e a força peso atuando:
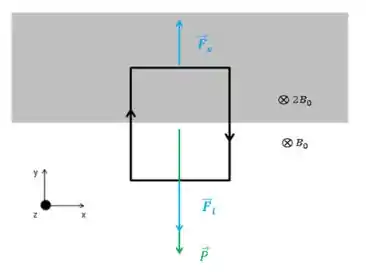
Como vimos, para a espira ficar parada,
O peso aponta na direção y para baixo, então
Então
Então a massa da espira que satisfaz essa condição é:
Passo 2
b)
opa! Agora a espira deu uma girada. Mas ainda queremos saber a mesa coisa. Tem pelo menos duas formas de fazer esse exercício. Uma, que tem que fazer mais contas, e outra que já serve de bizu para questões futuras. Vou mostrar esse bizu e explicar como seria a forma mais longa, beleza? A forma mais demorada é calcular a força magnética, através da formula:
Para cada segmento na espira que está em cada campo. Então você teria que fazer essa formula para 4 regiões, 2 com o campo e 2 com o campo . Note que, você teria que tomar cuidado com o , porque em nenhum dos segmentos ele está em uma das direções do eixo de referência, teríamos que decompor e então fazer o produto vetorial. Sacou? Bem, pensa aqui comigo, a força gerada pela componente vertical de seria nula para cada região. Porque, em uma parte a gente tá subindo e na outra, tá descendo. Olha aqui na figura:
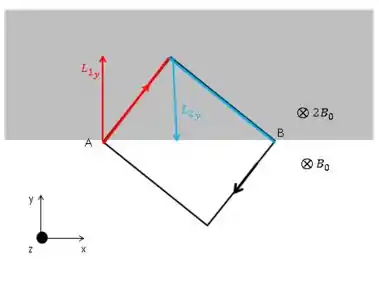
Mas o tanto que você subiu é igual ao tanto que você desceu, então como o campo magnético é uniforme, a força gerada por essas componentes de , quando somadas, dão zero. Mesma coisa acontece para a região de campo .
Então, poderíamos ver isso pelas contas, ia dar trabalho, mas íamos chegar a essa conclusão, ou então, podemos pensar nesse argumento e já calcular só a parte horizontal de . Que é a forma mais rápida.
Então, vamos lá!
Para a região com campo :
Onde
E é esse cara:
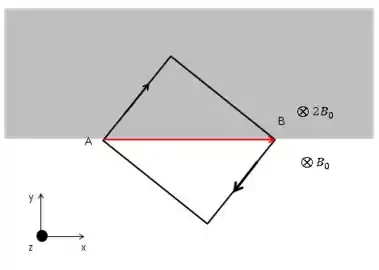
Portanto, pelo teorema de Pitágoras, como sabemos os outra lados da espira, temos:
E ele tá na direção x, sentido positivo, então:
E para a região com campo :
Onde
E o é:
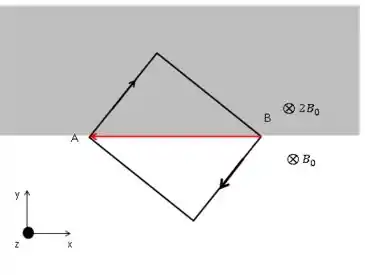
Notem que o vetor mudou de sentido pois agora a corrente vai de B para A, o oposto ao tínhamos antes.
Então
Beleza?
Então:
Então, a força resultante na direção y é:
Já coloquei igual a zero, porque é a mesma condição da letra a). tudo tem que estar em equilíbrio, paradinho.
Então:
A massa que satisfaz essa condição é:
Maravilha!!
Resposta
a)
b)