Uma espira é formada por dois segmentos de reta de comprimento e um trecho semicircular de raio , conforme ilustrado na figura. A espira está sujeita a um campo magnético uniforme dado por e a corrente percorre a espira no sentido indicado na figura.
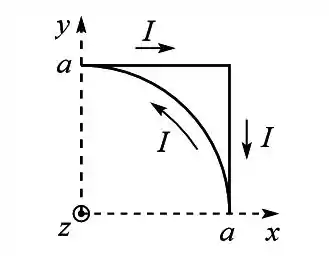
(a) Calcule o vetor força magnética sobre os segmentos retilíneos horizontal e vertical.
(b) Calcule o vetor força magnética sobre o trecho circular.
Passo 1
a) Bom, a expressão que nos dá a força magnética é a seguinte:
Segmento retilíneo horizontal:
Segmento retilíneo vertical:
Passo 2
(b) Já pro segmento circular, a parada fica um pouco mais séria, já que temos que fazer uma parametrização do
Parametrizando:
Derivando:
E então, pra achar a força:
Resposta
a) Horizontal: / Vertical:
b)
Exercícios de Livros Relacionados
Um condutor longo, rígido, retilíneo, situado sobre o eixo x , é percorrido por uma corrente de 5,0A no sentido negativo do eixo x . Um campo magnético B → está presente, dado por B → = 3,0 i ^ + 8,0
Um fio de 1,80 m de comprimento é percorrido por uma corrente de 13,0 A e faz um ângulo de 35,0 º º com um campo magnético uniforme de módulo B = 1,50 T . Calcule a força magnética exercida pelo campo
Uma linha de transmissão horizontal é percorrida por uma corrente de 5000 A no sentido sul-norte. O campo magnético da Terra ( 60,0 μ T ) tem a direção norte e faz um ângulo de 70,0 ° com a horizontal
Na Fig. 28-46, um fio metálico de massa m = 24,1 m g pode deslizar com atrito insignificante sobre dois trilhos paralelos horizontais separados por uma distância d = 2,56 c m . O conjunto está em uma
Um fio situado no eixo y , entre y = 0 e y = 0,250 m , é percorrido por uma corrente de 2,00 m A no sentido negativo do eixo. Na região existe um campo magnético não uniforme dado por B → = 0,300 T /