(A) na direção
(A) na direção
(A)4 na direção
(A) na direção
(A)
Passo 1
Essa é a fórmula do BILL.
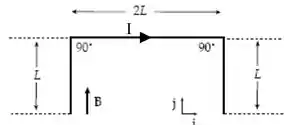
Como o seno de é nulo, somente a parte do fio perpendicular ao campo magnético vai influenciar. No caso a gente troca pelo comprimento do fio, que é :
Ficamos entre as letras (A) e (B).
Passo 2
A questão fala de direção mas na verdade, o termo mais adequado seria sentido...a direção é , mas temos que saber se o sentido é entrando no papel () ou saindo do papel .
Isso a gente faz pela regra da mão direita, escrevendo a equação na forma vetorial:
O vetor aponta para a direita. Fazendo a mãozinha, descobrimos que o campo está saindo do papel.
Resposta
Letra (B).
Exercícios de Livros Relacionados
Um condutor longo, rígido, retilíneo, situado sobre o eixo x , é percorrido por uma corrente de 5,0A no sentido negativo do eixo x . Um campo magnético B → está presente, dado por B → = 3,0 i ^ + 8,0
Um fio de 1,80 m de comprimento é percorrido por uma corrente de 13,0 A e faz um ângulo de 35,0 º º com um campo magnético uniforme de módulo B = 1,50 T . Calcule a força magnética exercida pelo campo
Uma linha de transmissão horizontal é percorrida por uma corrente de 5000 A no sentido sul-norte. O campo magnético da Terra ( 60,0 μ T ) tem a direção norte e faz um ângulo de 70,0 ° com a horizontal
Na Fig. 28-46, um fio metálico de massa m = 24,1 m g pode deslizar com atrito insignificante sobre dois trilhos paralelos horizontais separados por uma distância d = 2,56 c m . O conjunto está em uma
Um fio situado no eixo y , entre y = 0 e y = 0,250 m , é percorrido por uma corrente de 2,00 m A no sentido negativo do eixo. Na região existe um campo magnético não uniforme dado por B → = 0,300 T /