Um circuito que tem o formato de um triângulo equilátero de lado , está no plano e é percorrido por uma corrente constante, no sentido horário. O circuito está imerso em um campo magnético na direção (entrando na folha, como mostra a figura).
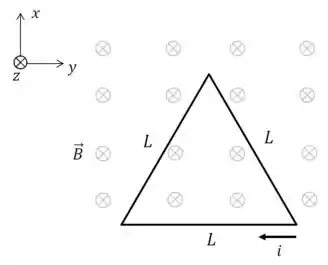
a) Mostre a direção e sentido da força magnética atuando em cada lado do circuito, através de um diagrama.
b) Calcule o módulo da força magnética em cada lado do triângulo.
c) Calcule o momento magnético do circuito.
d) Calcule o torque inicial sobre o circuito.
Passo 1
Então pessoal, nós temos aqui um fio percorrido por uma corrente e imerso em um campo magnético.
Nessa situação, a gente sabe que cada trecho do fio vai sofrer uma força dada por essa fórmula aqui:
Ou seja, temos que usar a regra da mão direita para encontrar a direção da força em cada caso.
Passo 2
Dê uma olhada no desenho (começando com o fio de baixo):
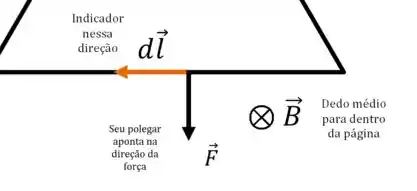
Aqui nós desenhemos no mesmo sentido da corrente que o enunciado descreveu. A força nesse trecho aponta para baixo.
Nos outros trechos, é só usar a mesma regra:
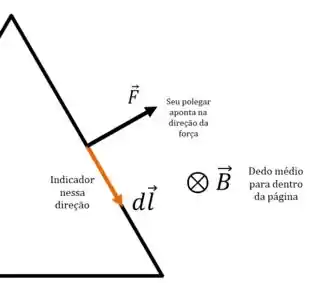
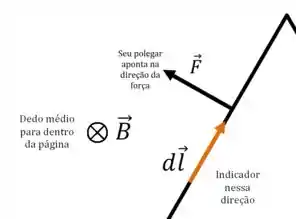
Beleza, então as forças são perpendiculares aos fios, sempre apontando para o lado de fora do triângulo. Resumindo tudo isso em um único diagrama:
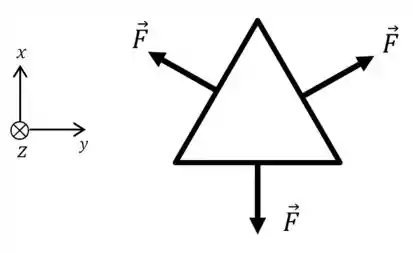
Passo 3
(b) Agora queremos calcular o módulo dessa força magnética em cada fio.
Bom, vamos voltar para a nossa fórmula de antes:
Como o campo está entrando na página, os vetores e são sempre perpendiculares, então o módulo daquele produto vetorial é:
Então, tirando o módulo dos dois lados daquela equação:
E agora integrando dois lados, com indo de até (já que estamos pensando em um fio só):
O campo magnético é constante ao longo do fio, e a corrente também, então podemos tirá-lo da integral:
Esse é o módulo da força em cada um dos três fios do triângulo.
Passo 4
(c) Agora queremos calcular o momento magnético do circuito. Vamos lembrar da fórmula para isso:
Nesse caso, é o momento dipolar magnético, é o número de espiras no circuito (bobina) e é a área de cada espira.
Aqui estamos lidando com um triângulo equilátero de lado , então a área é:
Além disso, a corrente foi dada no enunciado e o número de espiras é :
Mas o que é essa direção do vetor? Bom, a direção e o sentido do momento magnético são dados pela regra da mão direita.
Como a corrente percorre o circuito no sentido horário, você tem que girar os dedos da sua mão direita nessa direção, e então o seu polegar esticado vai dar a direção de :
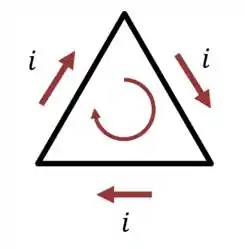
Quando você fizer isso, seu polegar deve estar apontando para dentro da página, ou seja, o momento magnético também aponta para dentro da página.
Pelo sistema de coordenadas que o enunciado deu, essa é a direção , então:
Passo 5
(d) Para finalizar, o enunciado pediu o torque inicial sobre o circuito.
A fórmula para esse torque é a seguinte:
Já temos uma fórmula para o nosso momento magnético , e como o campo magnético também está entrando na folha, podemos escrever ele assim:
Então o produto vetorial é:
Mas o produto vetorial de por é nulo, já que ele forma um ângulo de com ele mesmo:
E . Ou seja:
O torque inicial sobre o circuito é nulo.
Resposta
(a) Ver desenho.
(b) O módulo da força em cada um dos lados é .
(c) O momento magnético do circuito é .
(d) O torque inicial sobre o circuito é .