PUC-RIO – Física 3 2020.1 – P3– Questão 5
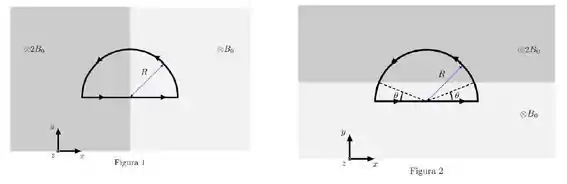
Uma espira semicircular de raio está posicionada entre duas regiões de campo magnético constante (nas Figuras 1 e 2, a região cinza-claro) e (nas Figuras 1 e 2, a região cinza-escuro). A espira é percorrida por uma correnteno sentido indicado nas Figuras 1 e 2. Observe que, na Figura 1, as metades da espira se encontram em regiões distintas. Calcule o vetor força magnética resultante na espira devido aos campos magnéticos de cada região, quando a espira se encontra:
- Posicionada como mostra a figura ;
- Posicionada como mostra a figura , onde o ângulo é .
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Vamos considerar que a espira é composta por duas partes nas regiões de campos constantes. Como o campo é constante ao longo de cada seção, podemos escrever a força magnética assim ó:
Aqui usei o vetor como o vetor deslocamento do ponto inicial da espira até o ponto final. Se chamarmos como o vetor deslocamento do lado direito, ou seja , a força será :
E chamando o vetor deslocamento associada ao lado esquerdo, a força fica assim:
E a força resultante é a soma das duas forças:
Passo 2
Letra (b):
Nesse item vamos aplicar o mesmo raciocínio feito anteriormente. Agora o vetor deslocamento na região inferior será e a força é:
Agora vamos à parte superior. Nessa parte, o vetor deslocamento é e a força é:
E a força resultante é a soma das duas forças:
E com temos que a força resultante é:
Beleza?
Pronto pra próxima questão? =)