UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 5b
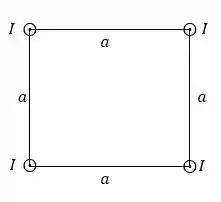
Quatro longos fios de cobre são paralelos entre si e estão dispostos em um quadrado de lado . Eles conduzem correntes iguais para fora da página, conforme mostrado na figura.
b) encontre a expressão literal para o módulo da força por metro sobre qualquer um dos fios. Substitua os valores para , e indique o valor da força.
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá?
Temos quatro fios, e escolhendo um deles para calcular a força por metro, precisamos determinar a influência dos outros três nesse outro fio. Vou escolher o fio inferior direito para calcular, mas você pode escolher qualquer outro e comparar o resultado! Vai ser o mesmo! Já que as correntes são as mesmas =)
Em relação ao ponto escolhido, usando a regra da mão direita, temos três campos (devido aos outros três fios):
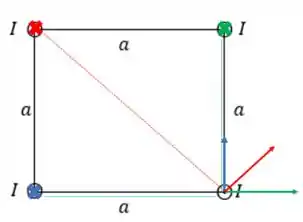
Para calcular a força, precisamos calcular primeiro o campo de cada fio. Então, vou usar a lei de Ampére, calcular o campo associado aos três fios, e achar o campo magnético resultante.
Como o campo é perpendicular à corrente, a força magnética é
E a força por unidade de comprimento de fio é
E com a expressão do campo, é só substituir os valores! Então a ideia é essa! Calcular o campo, jogar na força e substituir os valores!
Mas calma, vou fazer passo a passo com você!
Passo 2
A lei de Ampére para um fio a um ponto que está a uma distância do fio é:
Agora para cada fio, vamos ter um vetor diferente! Regatando do passo anterior o desenho dos campos magnéticos devido a cada um dos fios:
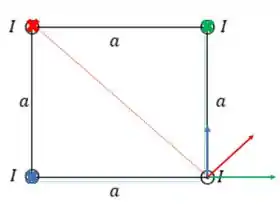
O campo do fio com um X azul é vertical para cima, então o vetor unitário que dá essa direção é o , e como a distância entre os fias é igual ao lado do quadrado então o campo devido a esse fio é:
Tudo bem até aqui?
O fio com X verde causa um campo na direção horizontal, então o vetor unitário que dá a direção é o , a distância entre os fios é o lado do quadrado então também. E aí o campo dele é
Já o vetor vermelho está na diagonal para cima. Um vetor unitário que tem essa direção é uma composição dos versores e :
E a distância entre os fios é igual a diagonal do quadrado então . Assim o vetor campo magnético do fio vermelho é:
Tranquilo?
Passo 3
O próximo passo é encontrar o campo resultante: basta somar todas as componentes:
O vetor campo resultante vai ser o módulo é a raiz da soma do quadrado das componentes:
Passo 4
Oba! Agora com a expressão do campo na mão, podemos calcular a força por metro! Lá do passo 1:
Então:
E agora é só substituir os valores:
,
Beleza?
Espero ter ajudado! Até a próxima!