UFRJ – Física 3 – 2020.2 – P5 – Exercício 5
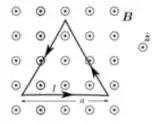
Temos um circuito condutor na forma de triângulo equilátero de lado , ao longo do qual flui uma corrente elétrica estacionária de intensidade e sentido como representado na figura abaixo. Tal circuito está sujeito a um campo magnético constante (estacionário e uniforme) , com sentido indicado na figura. Marque a opção que melhor corresponde à força magnética resultante sobre o circuito.
a)
b)
c)
d)
e)
Passo 1
Fala galerinha, beleza?
Eu sei que você sabe que quando uma partícula com carga se movendo com velocidade numa região com um campo magnético , aparece uma força dada por
Da mesma forma, quando temos um elemento infinitesimal de corrente num campo , aparece uma força infinitesimal:
Para chegar nessa expressão, é só fazer e .
Se você quiser achar a força no fio todo, basta integrar ao logo do fio. No caso do fio fechado (espira), a integral é fechada:
Passo 2
Agora vem a mágica! Como aponta na direção do fio e é perpendicular ao plano do fio, o vetor estará contido no plano da figura, mas será perpendicular ao fio. Quando consideramos as três porções do fio, é possível ver que a simetria do problema vai fazer com que essas forças se anulem, de modo que a força resultante será nula:
É possível mostrar, usando um pouquinho de cálculo vetorial, que para qualquer geometria a força magnética sobre um fio fechado sob ação de um campo magnético é nula. Isso é um assunto um pouco mais avançado e foge do escopo de física 3, mas achei legal falar para você que isso pode ser feito. Agora você já sabe e se aparecer na sua prova pode marcar sem peso na consciência 😉.
Alternativa B!
Resposta
Alternativa B.