Duas fontes pontuais, , estão localizados sobre o eixo à mesma distância da origem do sistema de coordenadas(ver figura). As fontes emitem ondas sonoras cujos deslocamentos são dados por:

é uma constante, são as distâncias de e ao ponto de observação, respectivamente, são medidos em metros e é medido em segundos.

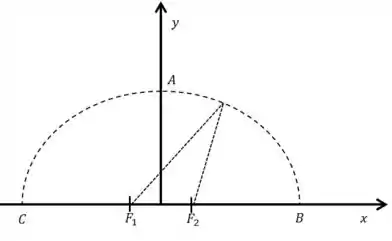
Efetuando-se medidas de nível sonoro sobre pontos localizados sobre o semicírculo mostrado na figura, com centro na origem e raio observou-se que a intensidade é nula em , aumenta até atingir um valor máximo em e volta a ser nulo em

1. Obtenha o número de onda e o comprimento de onda.
2. Obtenha o valor da constante de fase, da onda emitida pela fonte
3. Obtenha a distância entre as duas fontes.
4. Sabendo que a potência sonora emitida por cada fonte é igual a , calcule a intensidade e o nível sonoro(em no ponto caso apenas uma das fontes esteja emitindo. Considere
5. Calcule a intensidade e o nível sonoro em no caso em que as duas fontes estão emitindo simultaneamente.

Dados:

b)

Pra descobrir a fase, vamos usar o fato de que as ondas geram interferências totalmente destrutivas em .

Em , valem:

Onde é o raio e a distância das fontes até a origem.

Como a soma das ondas tem que ser nula, podemos dizer que:

Vamos seguir o mesmo procedimento em , lembrando-se de recalcular

Assim, por fim, temos as equações:

Vamos soma-las:

Agrupando oos termos iguais:

As duas somas de senos acima precisam dar zero, assim:

Vamos usar, agora, a relação abaixo:

Podemos aplicar em apenas uma das equações, já que a constante de fase é a mesma. Assim, aplicando na primeira:

Essa somaa precisa ser nula para qualquer tempo , então:

Pronto (:

c)

Precisamos descobrir o valor de ( já que a distância de cada fonte à origem vale a distância entre elas vale

Podemos usar a equação das interferências sonoras. Primeiro, aplicamos para o caso em que há um interferência totalmente destrutiva, como no ponto . Assim, a equação tem o formato:

Com:

Quanto vale Usando o valor de

Assim:

Assim:

Mas não sabemos o valor de Podemos então usar o ponto onde há interferência totalmente construtiva, o ponto

Nesse ponto, as distâncias até a circunferência são iguais, portanto:

Como a interferência é construtiva, o formtao da equação é:

Assim:

d)

Nesse caso, a intensidade pode ser calculada por:

Repara que aqui eu to usando a área de meia esfera, porque não temos onda em .

Assim, o nível sonoro será:

e)

Nesse caso, vamos considerar e vamos usar a equação abaixo pra calcular a intensidade da onda resultante, levando-se em consideração a diferença de fase:

Onde :

Assim:

Como a intensidade ali é máxima, não podemos deixar que :

Assim:

Assim:

Assim, o nível sonoro será: