Na figura abaixo, duas fontes sonoras e , separadas por uma distância , estão em fase e emitem ondas isotropicamente com potências e , respectivamente. Um ouvinte se encontra a uma distância da fonte , como mostra a figura. Considere a velocidade do som no ar igual a .
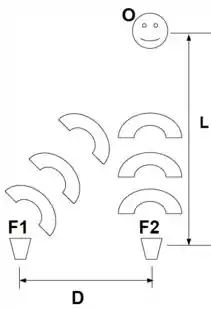
Calcule as intensidade e os níveis sonoros detectados pelo ouvinte , devidos a cada uma das fontes e , separadamente.
Passo 1
Para determinar a intensidade, precisamos lembrar da seguinte fórmula:
Onde é a distância entre a fonte e o ouvinte.
Para a fonte , temos:
Para a fonte , temos:
Passo 2
Para calcular o nível sonoro, devemos lembrar da sua fórmula:
Lembrando que .
Como a intensidade é a mesma para ambas as fontes, temos que:
Resposta
; ;
Exercícios de Livros Relacionados
Uma fonte produz uma onda senoidal de frequência angular 3000 r a d / s e amplitude 12 n m em um tubo de ar. O raio interno do tubo é 2 c m . ( a ) Qual é a taxa média com a qual a energia (soma das e
Uma onda sonora com uma frequência 300H z tem uma intensidade de 1,00μ W / m 2 . Qual é a amplitude das oscilações do ar causadas pela onda?
Em um certo ponto, duas ondas produzem variações de pressão dadas por Δ p 1 = Δ p m s e n ( ω t ) e Δ p 2 = Δ p m s e n ( ω t - ϕ ) . Nesse ponto, qual é a razão Δ p r / Δ p m , onde Δ p r é a amplitu
Uma fonte pontual emite 30,0W de som isotropicamente. Um pequeno microfone intercepta o som em uma área de0,750c m 2 , a 200m de distância da fonte. Calcule (a) a intensidade sonora nessa posição e (b
Qual é a razão entre o nível de intensidade de uma conversação normal e o nível de intensidade sonora de um murmúrio (a uma distância de 5,0 m )? (a) 10 3 (b) 2 (c) 10 - 3 (d) 1 2