Um espectador se encontra a de uma fonte sonora que produz ondas com frequência de e potência de .
a) Determine o nível sonoro percebido pelo espectador e localize (assinale) na figura abaixo o ponto correspondente à onda sonora produzida.
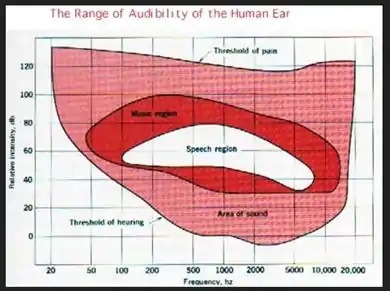
(b) Determine a potência da onda sonora recebida pelo espectador. Considere que o tímpano possui uma área de .
(c) Neste caso, qual a amplitude de vibração dos elementos do meio?
Dados: limiar de audibilidade:
Densidade do ar: .
Passo 1
a)
Primeiro de tudo, vamos ver o que é o nível sonoro.
Trata-se de uma função logarítmica da razão entre a intensidade medida e a intensidade mínima que somo capazes de ouvir. Ele é, geralmente, representado por
O limiar de audibilidade vale
Vamos descobrir então a intensidade percebida pelo espectador.
Onde é a potência e é a área da esfera cujo raio vai desde a fonte até o telespectador,
Então:
Vamos marcar essa região lá no gráfico. Temos no eixo y, e no eixo x.
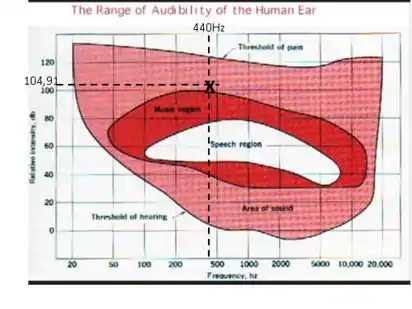
Passo 2
b)
Agora queremos a potencia recebida pelo tímpano.
A intensidade da onda que chega até o espectador é , e a área do tímpano é . Então a potência que chega até o tímpano é:
Prontinho!
Passo 3
c)
Agora ele quer a amplitude de oscilação da onda. Para um meio com densidade temos:
Onde é a intensidade da onda, é a velocidade de propagação da onda no meio e é a frequência angular dela, que pode ser escrita como no nosso caso, temos .
Resolvendo isso:
Maravilha!!
Resposta
a)
b)
c)