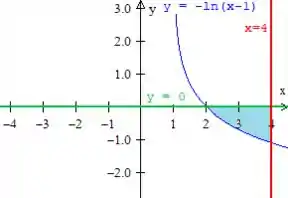
Considere a região plana definida por
Seja o sólido de revolução obtido pela rotação de em torno do eixo .
Letra a) Esboce abaixo a região plana .
Passo 1
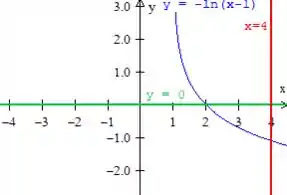
Letra (a) Então, para esboçar essa região, vamos começar entendendo melhor as três curvas que delimitam a região: , e .
Bem é uma reta paralela ao eixo e que passa por ; quanto , paralela ao eixo passando por em .
Pois então, basta a gente agora encontrar a cara dessa outra curva aí, essa , e basicamente esse nosso problema termina, pois a região vai estar dentro dessas coisas. ;)
Passo 2
Mas qual é a cara dessa função ?
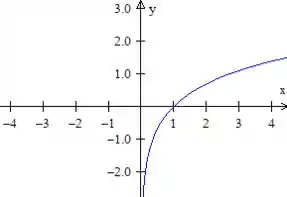
Pow, realmente a gente não tem a resposta dessa pergunta de primeira, porém a gente conhece a cara de uma muito parecida, :
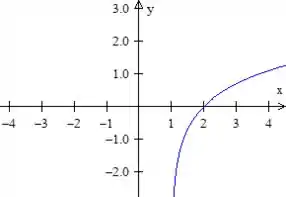
Mas subtrair um do argumento é pegar o gráfico e deslocar uma unidade pra direita em , dessa forma a gente consegue o gráfico de :
Quando multiplicamos por a função, a única coisa que muda é que invertemos o gráfico dessa forma aqui:
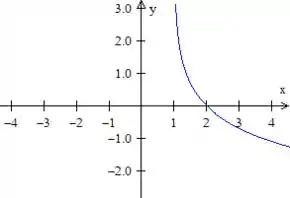
Passo 3
Agora jogando todas as três curvas de que falamos em um único gráfico, chegamos à região que precisávamos encontrar!
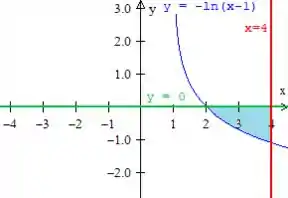
Resposta
Letra a)