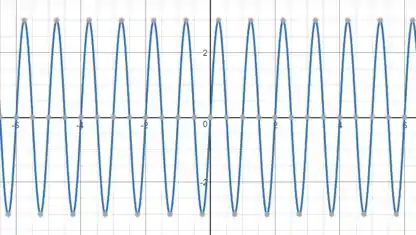
Esboce o gráfico da função
Passo 1
Perceba que não existem valores de que tornem essa função inexistente, logo o domínio é
Passo 2
Para determinar a imagem temos que lembrar que a função seno é uma função limitada entre
Como nossa função tem um multiplicando, podemos concluir que
Portando, a imagem é
Passo 3
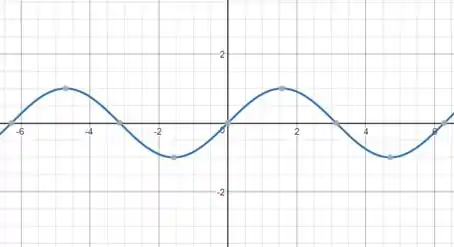
Vamos começar a fazer o esboço. Olhando pra função dada, a função mais genérica que parece com ela é:
Construiremos nosso gráfico a partir do gráfico dessa função, que é conhecido.
Passo 4
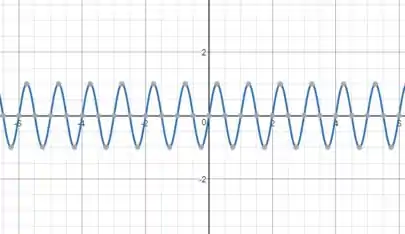
A primeira alteração feita na função acima é
Essa mudança aumenta a inclinação do gráfico em uma razão de . Sendo assim, o esboço se torna:
Passo 5
Passo 6
Passo 7
Finalmente, só resta multiplicar a função por .
Essa operação multiplica cada valor de por , isto é, cada valor de por . Assim, o gráfico se estica em unidades.
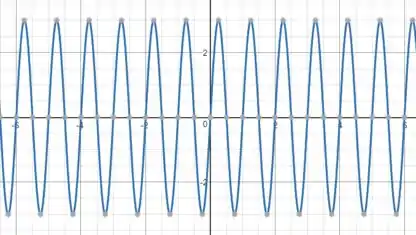
Resposta