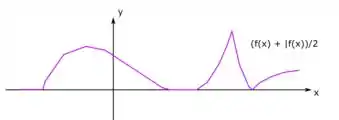
Nos exercícios 4. a 11., a partir do gráfico da função dado abaixo, esboce o gráfico da função dada.
10.
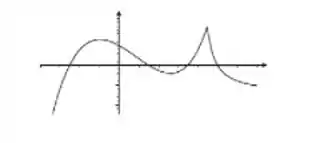
Passo 1
Opa! O exercício nos pede para olhar esse gráfico aqui
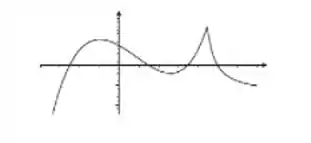
E a partir dele esboçar o gráfico da função . Bom, para fazer esse gráfico aí a gente tem que lembrar como que é o gráfico do módulo dessa função. Que no fundo é só espelhar para cima do eixo tudo que está para baixo. Assim ó:
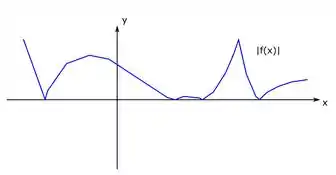
Isso a gente viu lá na questão 5 dessa lista ;)
A ideia aqui é colocar os dois gráficos juntos, ver como se comporta a soma dos dois e depois a gente tira a metade dos valores. Parece uma monte de coisa mas vocês vão ver que vai sair bem mais direto do que parece!
Então se liga como a gente vai fazer😊
Passo 2
Na prática a gente pode pensar na nossa função original
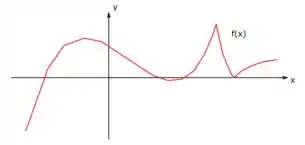
E agora vamos colocar junto desse gráfico, o gráfico de
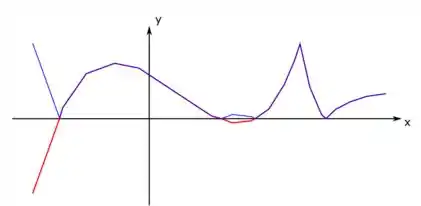
Olha só... A gente percebe que tem partes que os gráficos são iguais. E tem outras partes que os gráficos são iguais mas com sinais opostos, certo? Como a gente vai ter que calcular a soma desses gráficos, essas partes em que os sinais são opostos, quando somarmos as funções, vai dar:
E aí nesses trechos as funções morrem. Fica assim, ó:
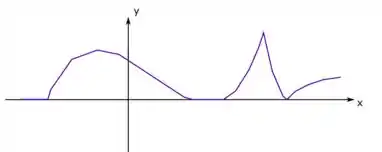
Passo 3
Agora a gente vai olhar o gráfico naqueles trechos em que . Se a gente tem isso, então:
Ou sejaaaaa... Nesses trechos, a soma das funções dividida por dois dá o gráfico da função original. Que maravilha hein! Então vamos ter:
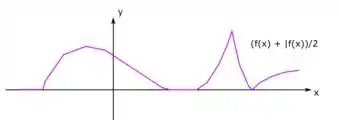
E aí resolvemos essa 😊 Vamos para a próxima?
Resposta