UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 19
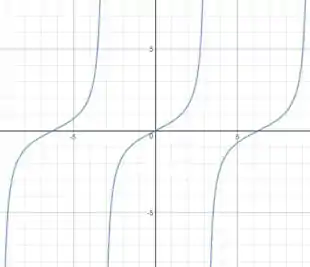
Esboce o gráfico da função
Passo 1
A função tangente existe para todo tal que
sendo um número inteiro.
Assim, o domínio da função
Pode ser dado por:
Passo 2
Para determinar a imagem temos que lembrar que a função tangente tem como imagem todos os reais. Portando, a imagem de é
Passo 3
Vamos começar a fazer o esboço. Olhando pra função dada, a função mais genérica que parece com ela é:
Construiremos nosso gráfico a partir do gráfico dessa função, que é conhecido.
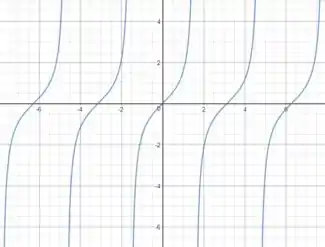
Passo 4
Queremos
Essa mudança reduz a inclinação do gráfico em uma razão de . Sendo assim, o esboço se torna:
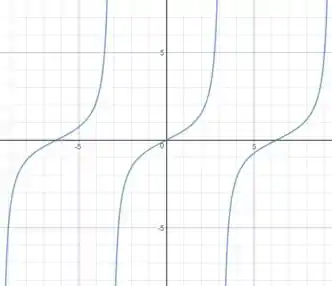
Passo 5
Passo 6
Resposta
Exercícios de Livros Relacionados
Se f( x ) = 3 x 2 - x + 2 , encontre f ( 2 ) , f - 2 , f ( a ) , f ( - a ) , f ( a + 1 ) , 2 . f ( a ) , f ( 2 a ) , f ( a 2 ) , f a 2 e f ( a + h ) .
Um balão esférico com raio de r centímetros tem o volume V r = 4 3π r 3 . Encontre uma função que represente a quantidade de ar necessária para inflar o balão de um raio r até um raio r + 1 centímetro
Uma estrela variável é aquela cujo brilho alternadamente cresce e decresce. Para a estrela variável mais visível, Delta Cephei, o período de tempo entre os brilhos máximos é de 5,4 dias, o brilho médi
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção 1.2 e então aplicando as transformações apropriadas. y = 1 4 t g x - π 4
Classifique cada função como uma função potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial ou função logarítmi