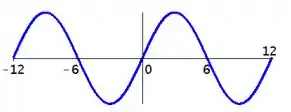
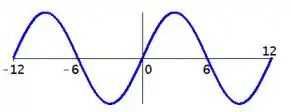
A figura abaixo mostra o gráfico da função trigonométrica
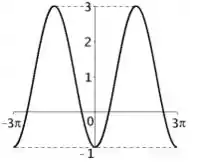
- Determine uma possível expressão para .
- Seja o período da função . Esboce abaixo o gráfico da função no intervalo. Indique em seu desenho as abscissas dos pontos interseção do gráfico de com o eixo .
- Determine os valores de para os quais
Passo 1
Letra a) Pow! Se trata aqui nesse problema de uma questão de manipulações com os gráficos já conhecidos.
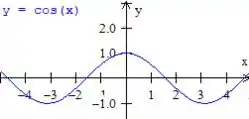
A primeira coisa que a gente deve notar aí é que esse gráfico se parece muito com o gráfico de um cosseno
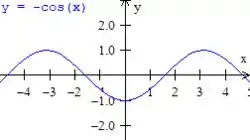
Porém com um menos na frente para ele ter um pico nos negativos:
Como a gente pode observar, esse gráfico sofreu um alongamento na horizontal de um termo :
Ele também foi esticado na vertical por um termo :
E por fim, a gente observa que ele se deslocou pra cima unidades:
Agora basta determinar esses termos e o nosso problema acaba. Bora?!
Passo 2
Se a gente notar bem, vamos perceber que o gráfico que a gente quer determinar, basicamente dobrou de comprimento, pois a sua amplitude é , duas vezes maior que a amplitude do cosseno normal. Logo a gente pode falar que esse termo
Quanto ao termo , notamos no gráfico que tem um período de , podemos encontrar pela sua relação com o novo período :
O termo , basta a gente reparar que o eixo central do cosseno está deslocada uma unidade, logo .
Portanto, a função que a gente procura é:
Passo 3
Letra b) Repare que nesse gráfico apenas temos uma mudança na horizontal da função seno. Logo, antes de mais nada, a gente deve buscar o período dessa nova função cosseno.
Pela relação do período com o termo , podemos encontrar o período dessa função:
Como nesse caso,
Passo 4
Para a gente encontrar as abscissas, basta a gente fazer e verificar as interseções com o eixo dentro desse intervalo .
Note que esse seno zera em múltiplos de , logo, dentro desse intervalo ele zerará em :
Passo 5
Letra c) Queremos aqui analisar o sinal da função . Pra isso vamos analisar separadamente o sinal da função e da .
Quanto a , devemos buscar as suas interseções com o eixo dentro do intervalo , basta fazer :
Isolando o cosseno...
Ou seja
Dentro do intervalo , notamos que só existe dois valores que zeram a função , logo basta encontrar os dois primeiros valores desse arco-cosseno: e , logo
Ou seja
Passo 6
Quanto a , já sabemos que ela vale zero em , 6 e 12. Porém, quem são esses angulos em radianos mais ou menos?
Pra fazer isto, bastamos ver a relação entre os angulos em radianos e ângulos normais em 12, 6, e 0 utilizando a regra de três :
Logo, notamos que o arco , está fora do intervalo que queremos avaliar, mas do arco até esse , temos o valor de negativa.
Passo 7
Pela análise dos dois gráficos, podemos concluir que

Fazendo a divisão de um pelo outro, notamos que
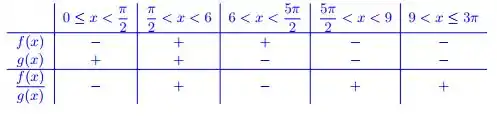
nos intervalos de e