Seja uma função real que tem o gráfico abaixo, onde . Por exemplo, no gráfico abaixo, para , assume o valor como no ponto destacado.
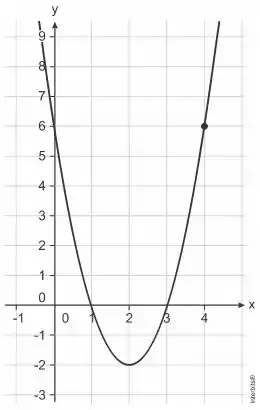
Sabendo disso, esboce o gráfico de e encontre os valores de para os quais a mesma assuma valor mínimo
Passo 1
A primeira coisa que vamos fazer é o módulo da função . Quando a gente faz isso, a gente transforma tudo que é negativo em positivo, ou seja, toda a parte abaixo do eixo no gráfico, a gente vai espelhar para cima. Ele vai ficar assim ó:
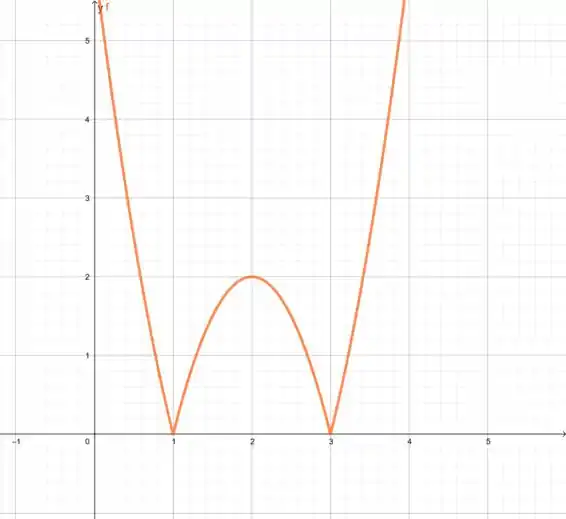
Show?
Passo 2
Agora, pense no seguinte: Se estamos somando a essa nossa nova função, basta que a gente suba casas com ela. Sempre que a gente fizer um somatório, a gente vai deslocar o gráfico de acordo com o somatório feito. Então ficaremos com o nosso gráfico assim:
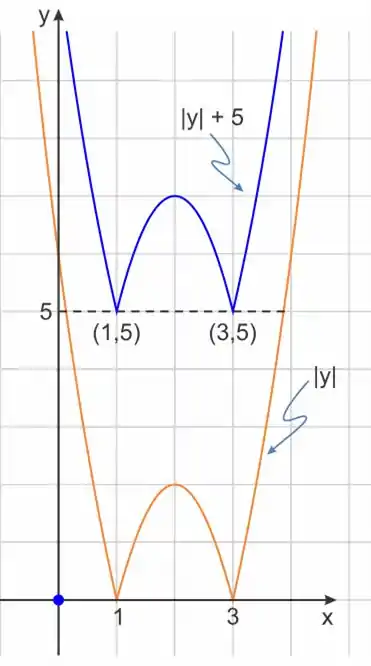
Muito bem, percebemos que a nossa expressão gerará pontos mínimos, os pontos . Ou seja, os valores de para os quais a função assume valor mínimo são ou
Resposta
ou