UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 13
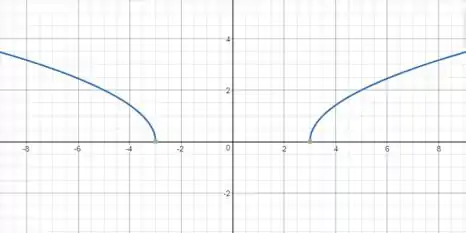
Esboce o gráfico da função
Passo 1
Para começar um esboço de gráfico, uma boa estratégia é começar verificando se a função tem pontos em que não está definida. Por exemplo, no caso de raízes quadradas o radicando nunca pode ser negativo. Por isso, vamos ver para quais valores a função dada existe, ou seja, tem radicando positivo.
Logo, ao esboçarmos o gráfico, sabemos que ele só existirá quando ou .
Passo 2
Vamos começar a fazer o esboço. Olhando pra função dada, pense na função mais genérica que parece com ela. Seria essa aqui ne?
O gráfico dessa função é simples de esboçar, basta substituir alguns valores e marcar no plano cartesiano. E ele fica assim:
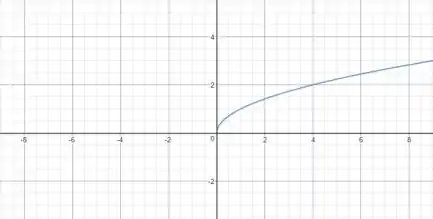
O gráfico que queremos será construído a partir desse.
Passo 3
Na função acima o só pode assumir valores positivos. Na função que queremos é diferente porque o está dentro de um módulo. Nesse caso, o pode ter valores positivos e negativos, pois o módulo impede que o radicando fique negativo. O que de fato vai acontecer acrescentando o módulo é que o gráfico acima será espelhado em torno do eixo . Então, esboço de
Fica assim:
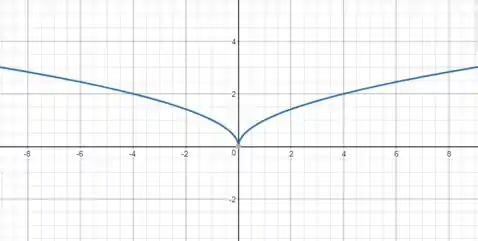
Passo 4
Estamos chegando perto do que vai ser o resultado final. Agora faremos o gráfico de
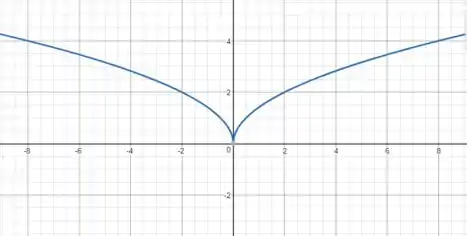
O que essa multiplicação fará com o gráfico anterior é estica-lo numa proporção de uniddes. Substituindo alguns valores encontramos o seguinte esboço:
Passo 5
Agora só falta subtrair o 6 do radicando. Queremos a função
O que essa operação irá fazer com o gráfico anterior é deslocar o gráfico em 3 unidades. Como a parte negativa é o espelho da parte positiva, esta andará 3 unidades para a direita e aquela andará unidades para a esquerda.
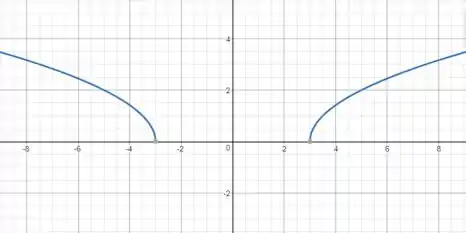
Resposta
