UFES – Cálculo 1 – Listas de Estudos UFES – Lista 2
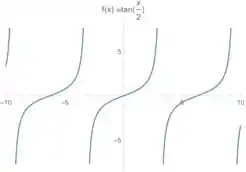
Nos exercícios 18 a 21 determine o domínio, a imagem e esboce o gráfico da função dada.
19.
Passo 1
Fala aí pessoal, tudo certinho??O problema está nos dando essa função daqui
E está nos pedindo para determinar o domínio, que é o conjunto dos possíveis valores de que podem entrar nessa função; a imagem, que são os possíveis valores que a nossa função pode assumir; e ele quer também um esboço do gráfico.A nossa estratégia vai ser a seguinte: Vamos determinar o domínio olhando as restrições que a nossa função pode ter... Por exemplo, não podemos dividir por zero, tirar raiz de números negativos e etc. A imagem a gente determina conhecendo um pouco da função. Por exemplo, o seno só nos dá valores entre e , certo?O esboço a gente faz olhando uma função que a gente já conhece o gráfico e ir fazendo transformações em cima desse gráfico para a gente obter a cara da nossa função.
Como na nossa função temos uma tangente aparecendo, vamos lembrar que o gráfico dessa função é esse cara aqui:
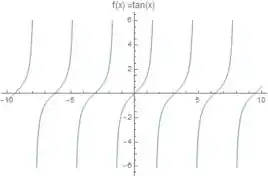
Então vamos lá resolver esse problema 😊
Passo 2
Vamos começar encontrando o domínio da nossa função
Para falar sobre o domínio é melhor a gente escrever a tangente como sendo:
OPA! Como temos uma fração, sabemos que o denominador tem que ser diferente de zero:
Lembrando que o cosseno é nulo para qualquer múltiplo inteiro de temos que:
Onde é
Dessa forma o domínio da função é:
Passo 3
Para ver a imagem temos que lembrar que a função tangente pode nos dá qualquer valor real. É só olhar o gráfico da tangente que a gente observa que ela não tem nenhuma limitação vertical. Ou seja, a imagem dessa função é qualquer valor real:
Passo 4
Agora, para o esboço a gente pode fazer uso do gráfico de :
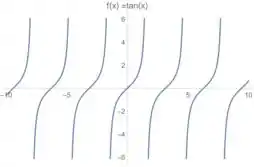
A gente só não pode esquecer que temos no argumento!
O papel desse é dobrar a distância entre as repetições do gráfico. No fundo é como se a gente esticasse horizontalmente essas cobrinhas que aparecem no gráfico da tangente.Então se antes eu tinha duas figuras dessas de até . Agora a gente tem uma só:
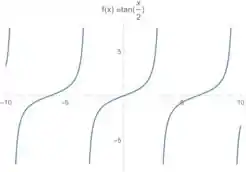
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
