Dado o gráfico de , associe cada expressão de com o seu gráfico e justifique suas escolhas.
a)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu alguns gráficos:
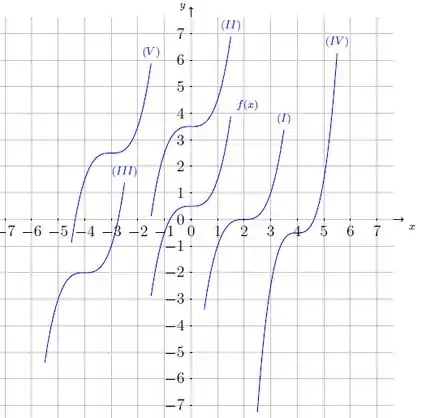
E nos deu uma função , a qual ele pediu pra gente associar com algum desses gráficos da figura acima. Percebe que o tá ali no meio? É importante a gente perceber que a nossa função está associada com o e o que tá acontecendo graficamente é que esse está se deslocando na vertical e na horizontal, ali no plano cartesiano.
Tá, mas como a gente identifica o deslocamento que a nossa função tá fazendo? A gente identifica através da lei de formação da função. Por exemplo, de eu tiver uma constante positiva e:
Então, o gráfico de foi deslocado em unidades para cima, porque cada coordenada vai ficar acrescida de um número . Vamos ver o que acontece nesse caso.
Passo 2
Para a nossa função:
A nossa constante é igual a . Isso significa que o gráfico de foi deslocado em unidades para cima. E qual a curva que está unidades para cima em relação a no gráfico?
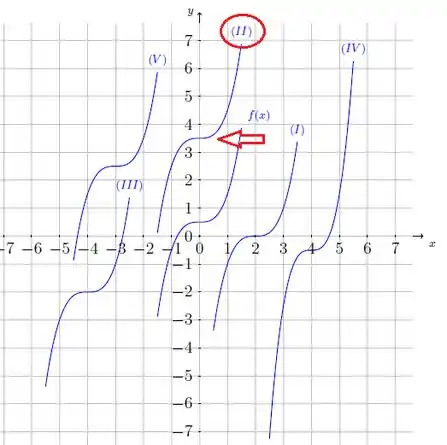
A curva , portanto, essa é a nossa resposta.
É isso, galera! Encerramos o exercício! 😉