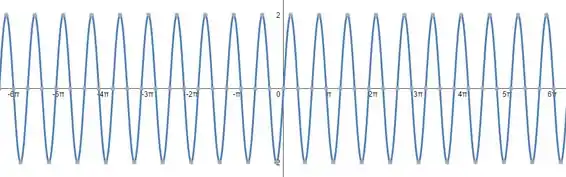
Construir os gráficos das seguintes funções definidas em :
Passo 1
- Temos que o gráfico da função cosseno é dado por
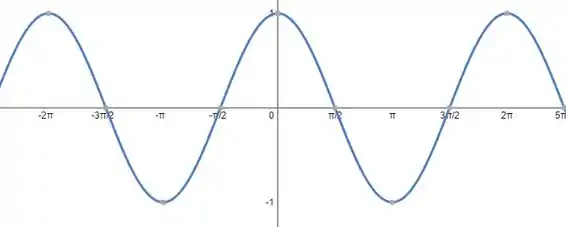
Passo 2
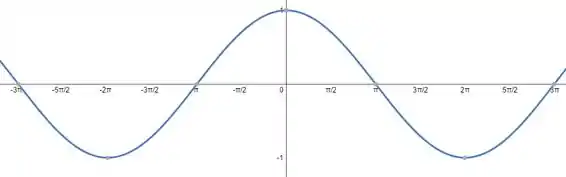
Agora multiplicamos por no cosseno e teremos porém,o período da função vai mudar, saca só!
O período pode ser calculado por , sendo o que multiplica o , teremos:
Desta forma, estaremos esticando a nossa função ao dobro no eixo x.
Logo o gráfico da nossa função vai ser:

Passo 3
b)
O que fazer aqui?Molezinha!
Temos uma transformação do tipo com .
Desta forma estaremos encolhendo o nosso gráfico em 3 vezes no eixo y
O domínio continua o mesmo, pois não alteramos o valor de . Mas a imagem se torna o intervalo que é a imagem da função cosseno, que é dividida por 3. Assim, o nosso gráfico será:
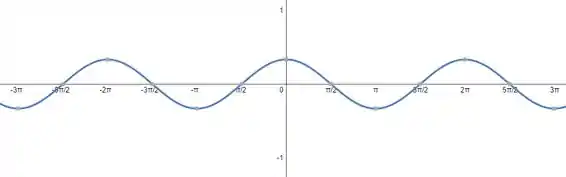
Passo 4
c)
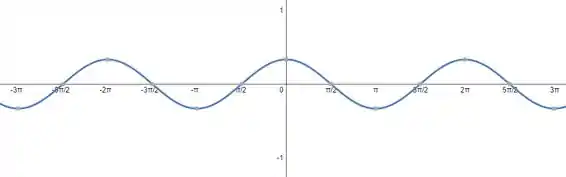
Bom, como multiplicamos a função seno por temos que a imagem vai se tornar o intervalo pelo mesmo motivo da letra b). Assim a nossa função vai esticar em duas vezes o seu tamanho no eixo y.
Além disso também temos uma transformação do tipo com . Desta forma, estaremos diminuindo o período da função em vezes, passando a ser .
Com isso, estaremos encolhendo a nossa função em vezes no eixo x.
Desta forma, vamos ter o gráfico que é a nossa resposta final.
:D
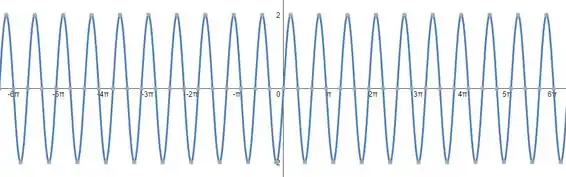
Resposta
b)
c)