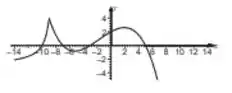
A partir do gráfico da função dado abaixo, esboce o gráfico da função dada.
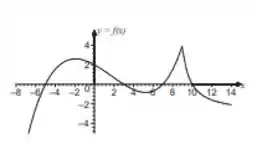
Passo 1
O sinal negativo antes do vai provocar uma mudança interessante. Veja esse exemplo, imagine a função . Vamos ver seu valor quando :
Agora seu valor quando
Agora veja o que ocorre se fizermos .
Para ,
Para ,
Então, se usarmos um positivo, levará ao valor da função para . E se usarmos um negativo, levará ao valor da função para .
Passo 2
No gráfico essa mudança irá se manifestar da seguinte maneira: a parte do gráfico onde é positivo será rebatida em torno de e se tornará a parte do negativo. E a parte onde é negativo será rebatida em torno de e se tornará a parte do positivo. Fica assim:
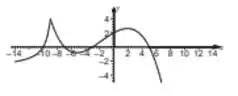
Resposta