UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 21
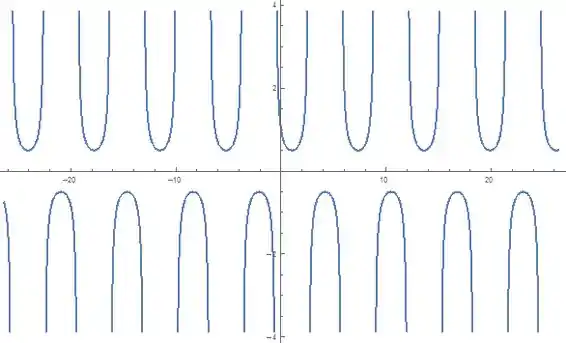
Determine o domínio, a imagem e esboce o gráfico da função dada.
Passo 1
A função secante tem domínio igual ao cosseno, com exceção do ponto que zera o denominador:
Que ocorre em:
Onde essa aparece porque a função é periódica. Dessa maneira:
Passo 2
Quanto a imagem, ainda pela definição, temos que:
Como:
Essa razão será sempre maior que ou menor que sem outras restrições, dessa maneira a imagem será:
Passo 3
Temos duas coisas aqui, uma constante que multiplica a secante. Essa constante é e, uma vez menor que , contrai pela metade o gráfico da secante.
Para o argumento, temos uma subtração por que nada mais é que o deslocamento do gráfico da secante unidades para direita.
Passo 4
Sendo o gráfico da secante:
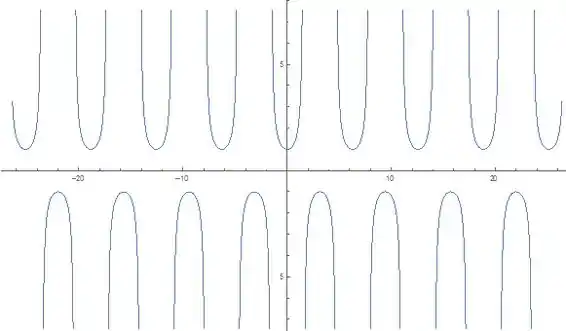
Contraindo pela metade:
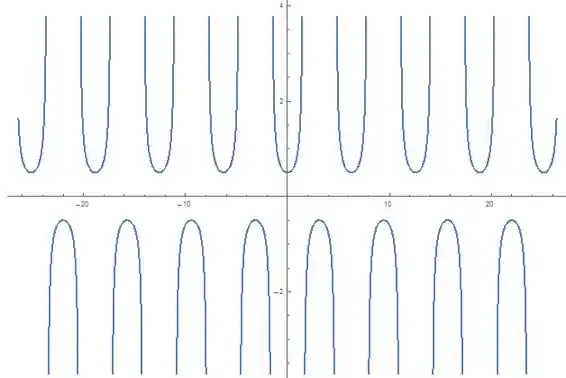
Deslocando para à direita :
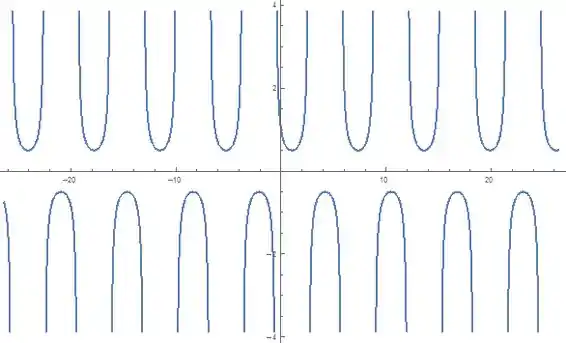
Resposta
Exercícios de Livros Relacionados
Se f( x ) = 3 x 2 - x + 2 , encontre f ( 2 ) , f - 2 , f ( a ) , f ( - a ) , f ( a + 1 ) , 2 . f ( a ) , f ( 2 a ) , f ( a 2 ) , f a 2 e f ( a + h ) .
Um balão esférico com raio de r centímetros tem o volume V r = 4 3π r 3 . Encontre uma função que represente a quantidade de ar necessária para inflar o balão de um raio r até um raio r + 1 centímetro
Uma estrela variável é aquela cujo brilho alternadamente cresce e decresce. Para a estrela variável mais visível, Delta Cephei, o período de tempo entre os brilhos máximos é de 5,4 dias, o brilho médi
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção 1.2 e então aplicando as transformações apropriadas. y = 1 4 t g x - π 4
Classifique cada função como uma função potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial ou função logarítmi