UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 15
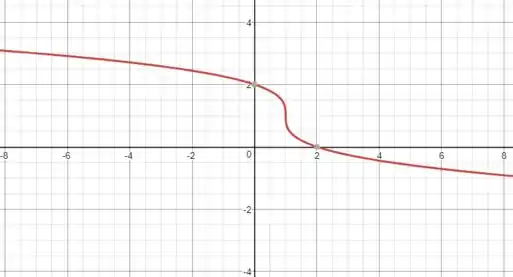
Esboce o gráfico da função
Passo 1
Observando bem a função, é possível perceber que não existem valores de que tornem essa função inexistente. A raiz é uma raiz cubica, por isso não há restrições para os valores que estarão dentro dela.
Passo 2
Vamos começar a fazer o esboço. Olhando pra função dada, a função mais genérica que parece com ela seria:
Construiremos nosso gráfico a partir do gráfico dessa função, que é simples de esboçar, basta substituir alguns valores e marcar no plano cartesiano. E ele fica assim:
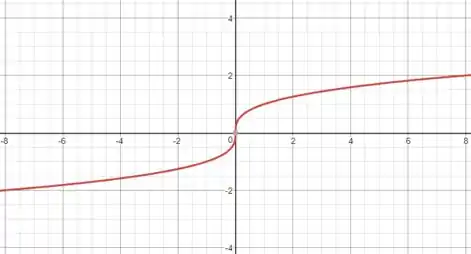
Passo 3
A primeira alteração feita na função acima é a mudança de sinal de . Ficamos com:
O sinal negativo transforma que era negativo em positivo e vice-versa. Assim, a função será refeltida em torno do eixo , resultando no seguinte gráfico:
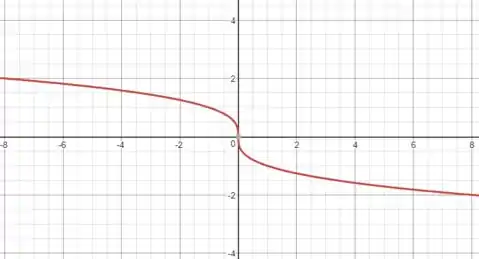
Passo 4
Passo 5
Passo 6
Agora temos que somar ao valor dentro da raiz.
Isso faz com que o gráfico seja transladado unidade para a direita.
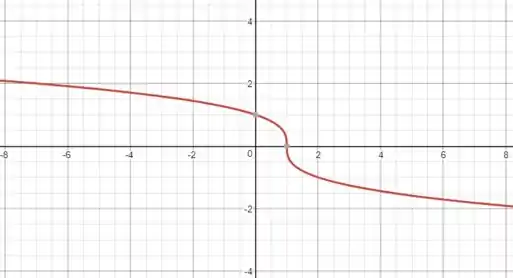
Passo 7
Finalmente, só resta somar à função .
Essa operação faz com que o gráfico suba uma unidade em relação ao eixo .
Portanto, o gráfico da função é:
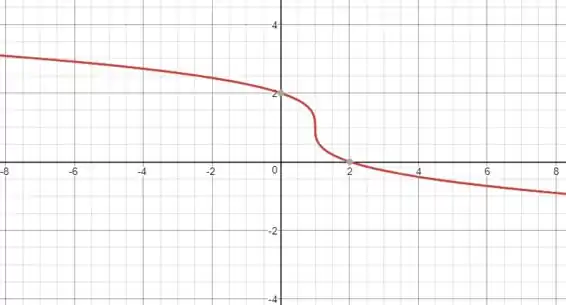
Resposta
