Nos exercícios 18 a 21 determine o domínio, a imagem e esboce o gráfico da função dada.
20.
Passo 1
Fala aí pessoal, tudo certinho??O problema está nos dando essa função daqui
Onde o enunciado nos fala que o só existe dentro do intervalo , e nos pede para determinar o domínio, que é o conjunto dos possíveis valores de que podem entrar nessa função; a imagem, que são os possíveis valores que a nossa função pode assumir; e ele quer também um esboço do gráfico.A nossa estratégia vai ser a seguinte: Vamos determinar o domínio olhando as restrições que a nossa função pode ter... Por exemplo, não podemos dividir por zero, tirar raiz de números negativos e etc. A imagem a gente determina conhecendo um pouco da função. Por exemplo, o seno só nos dá valores entre e , certo?O esboço a gente faz olhando uma função que a gente já conhece o gráfico e ir fazendo transformações em cima desse gráfico para a gente obter a cara da nossa função.
Como na nossa função temos uma função seno aparecendo, vamos lembrar que o gráfico dessa função é esse cara aqui:
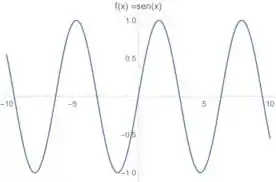
Então vamos lá resolver esse problema 😊
Passo 2
Vamos começar encontrando o domínio da nossa função
Como a nossa função não possui nenhuma restrição, qualquer valor de pode entrar nessa função sem problema algum. A única coisa que a gente tem que lembrar é que o enunciado já travou os valores de para o intervalo . Então o domínio vai ser:
Passo 3
Para ver a imagem temos que lembrar que a função seno pode nos dar um valor máximo de e o mínimo de . Isso acaba restringindo a nossa imagem. Vamos usar esses resultados nessa expressão:
Para o maior valor do seno, teremos:E para o menor valor do seno a gente tem:
Nessa última equação a gente obteve o maior valor possível da nossa expressão e por se tratar de um módulo o mínimo é 0. Então a imagem dessa função é dada por:
Passo 4
Agora, para o esboço a gente pode fazer uso do gráfico de :
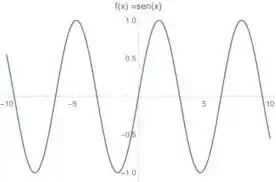
A gente só não pode esquecer que temos no argumento!
O papel desse é dobrar a distância entre as repetições do gráfico. No fundo é como se a gente esticasse horizontalmente esse gráfico.Então se antes eu tinha uma subida e uma descida de até . Agora a gente tem uma subida só:
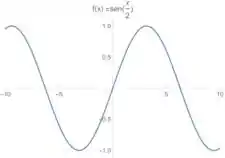
Passo 5
Outra transformação que surge é que precisamos subtrair dessa função que a gente obteve o gráfico. Isso é uma transformação do tipo:
No esboço, isso é a mesma coisa que andar verticalmente o gráfico para baixo unidades. Então a gente fica com isso aqui:
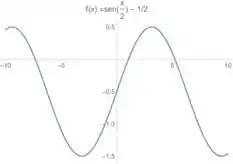
Passo 6
A última coisa que falta é tirar o módulo de tudo isso
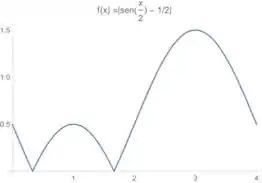
No esboço, isso é a mesma coisa que espelhar tudo que está para baixo do eixo (valores negativos da função) para cima (valores positivos da função). Então aquelas voltinhas que estão para baixo, vão ficar para cima. Assim ó:
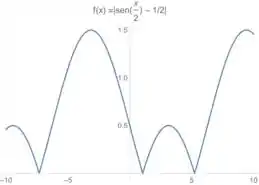
Mas cuidado!! O enunciado nos fala que a gente só tem valores de no intervalo de:
Ou seja, temos que restringir esse gráfico para esses valores de , então temos:
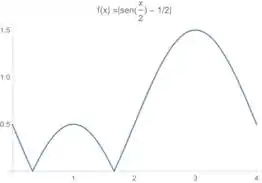
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta