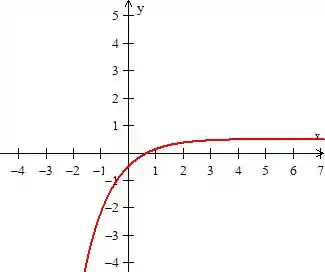
Nos exercícios a esboce o gráfico da função.
5)
Passo 1
Cara, nesse problema, poderíamos resolvê-lo de duas maneiras:
1º - Fazendo um monte de passo a passo encontrando domínio, intervalos de crescimento, etc.
2º - Fazer utilizando transformações de gráficos que já conhecemos.
A primeira maneira de se resolver é interessante quando temos uma função absurdamente complicada e que não temos uma noção muito clara de quem ela poderia ser. Mas, em casos que conseguimos dizer por alto qual é a cara da função, o segundo método é mais rápido.
Como conhecemos bem a cara da função ...
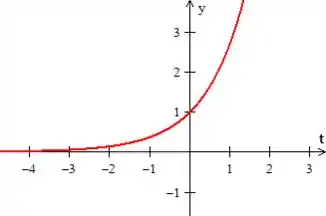
Podemos trabalhar um pouco com ela para chegar na que queremos...
Bora? :D
Passo 2
Man, quando invertemos o sinal de todo o argumento da função, o que fazemos na verdade é inverter o gráfico inteiro ao redor do eixo da função (o eixo ). Como se girássemos a função ao redor desse eixo. Logo, se o gráfico de é
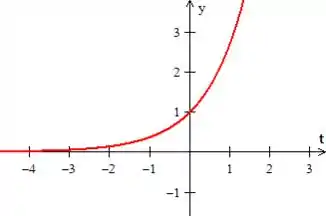
O gráfico de será...
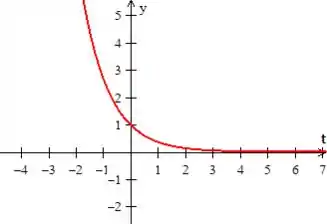
Passo 3
Invertendo o sinal agora da função (e não do argumento ),f azemos o mesmo giro de reflexão, mas agora ao redor do eixo do argumento , saca?
Então gráfico de , será
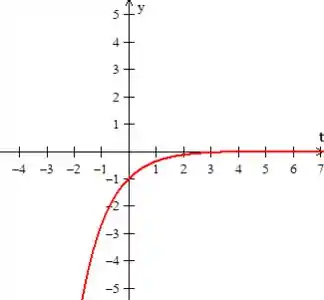
Passo 4
Quando somamos em toda a função, o que devemos fazer com o gráfico é desloca-lo meia unidade pra cima, ficando...
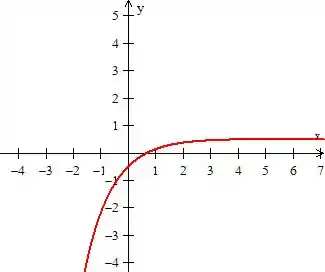
E esse é o gráfico que está estávamos procurando de . Viu como brincando como um gráfico conhecido chegamos bem mais rápido :D
Resposta