A função com a e b reais, representada graficamente a seguir, intersecta o eixo y no ponto de coordenadas (0, -1) e tem valor máximo . Qual é o valor da soma ?
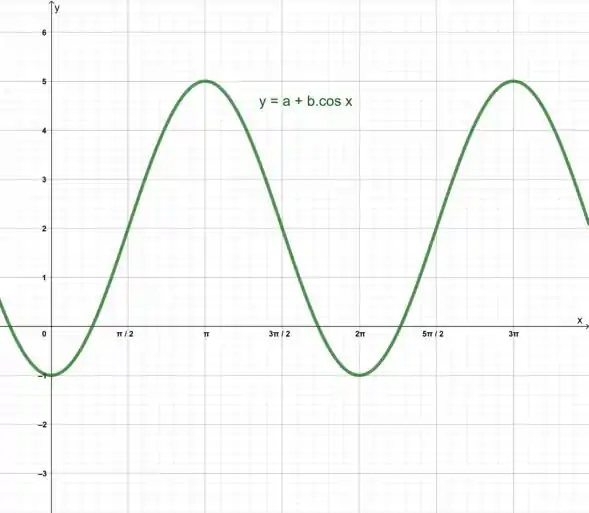
Passo 1
Sabemos que o “a” da nossa função apenas vai transladar nosso gráfico para cima ou para baixo, enquanto o “b” vai nos mostrar o quanto se a função foi ampliada de tamanho(duplicou, triplicou, etc)
Observe que o nosso gráfico está com um período indo de -1 a 5, ou seja, está abrangendo 6 casas, enquanto o gráfico de cosx abrange apenas 2 casas. Isso significa que triplicamos o valor da nossa função.
Agora observa o que acontece quando multiplicamos a nossa função por -1
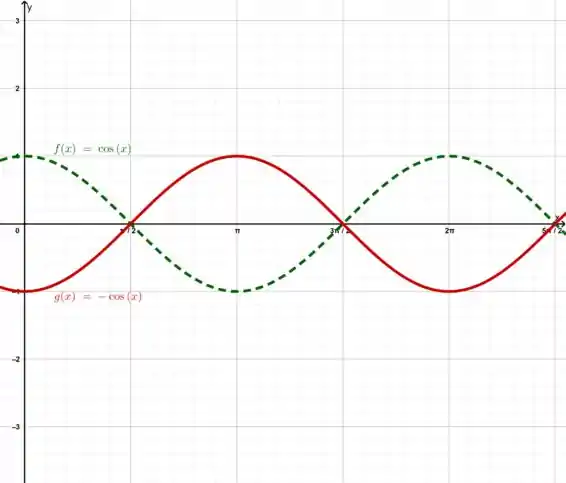
Nos invertemos o sentido da nossa função, isso acontece com a nossa função.
Sendo assim, o valor de b será -3.
No entanto, se fizermos o gráfico da função , teremos o gráfico em vermelho abaixo.
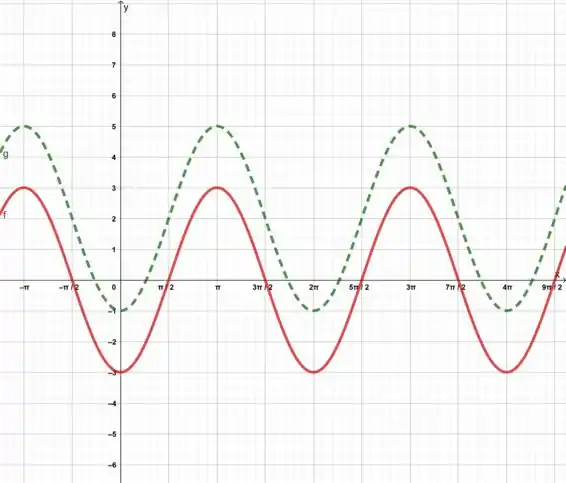
Mas queremos chegar no gráfico que está de verde e tracejado.
Ele está duas casas acima do outro, certo?
Então basta somarmos 2 a ele. Isso significa que
A nossa função então é :
Com
Show?
Passo 2
Agora ficou fácil, vamos achar o valor da expressão pedida no enunciado
Nossa resposta então será igual a 4.