Dado o gráfico de , associe cada expressão de com o seu gráfico e justifique suas escolhas.
b)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu alguns gráficos:
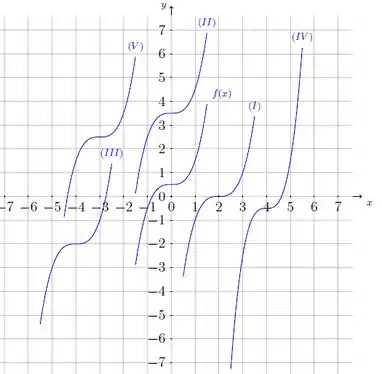
E nos deu uma função , a qual ele pediu pra gente associar com algum desses gráficos da figura acima. Percebe que o tá ali no meio? É importante a gente perceber que a nossa função está associada com o , e o que está acontecendo graficamente é que esse está se deslocando na vertical e na horizontal, ali no plano cartesiano.
Tá, mas como a gente identifica o deslocamento que a nossa função tá fazendo? A gente identifica através da lei de formação da função. Por exemplo, se eu tiver uma constante positiva e:
Então, o gráfico de foi deslocado em unidades para cima, porque cada coordenada vai ficar acrescida de um número . Mas, e se essa constante estiver sendo subtraída:
Então, o gráfico de estará sendo deslocado unidades para baixo. E se eu colocar esse dentro do argumento da função? Assim:
Então, a gente vai tá mexendo em um valor do eixo , isso significa que o gráfico vai tá se deslocando na horizontal. Nesse caso, ele se desloca pra direita, porque tudo vai acontecer unidades depois, então o gráfico de vai está unidades “atrasado”.
Usando a mesma lógica, conhecendo o gráfico de , o gráfico de é obtido a partir do deslocamento de em unidades para esquerda.
Sabendo de tudo isso, a gente pode olhar pra nossa função e ver em qual caso ela se encaixa. Vamos lá!
Passo 2
Para a nossa função:
A nossa função tem dentro do argumento a constante . Como ela está sendo subtraída, nós sabemos que a função vai estar deslocada unidades para direita.
Além disso, a gente tem a constante sendo subtraída do lado de fora da função. Olhando lá nos casos do passo , a gente vê que isso significa que o gráfico de foi deslocado em unidade para baixo.
Só falta a gente avaliar o que está multiplicado . Ela não se encaixa em um caso de deslocamento vertical ou horizontal, então qual modificação ela está fazendo na função?
Quando a gente tem uma constante maior do que multiplicando a função, ela vai provocar uma expansão vertical no gráfico de . Então, para o nosso caso, o gráfico está sendo expandido também em unidades.
Juntando todas essas informações, qual é o gráfico da função ? Olhando no gráfico, nós temos:
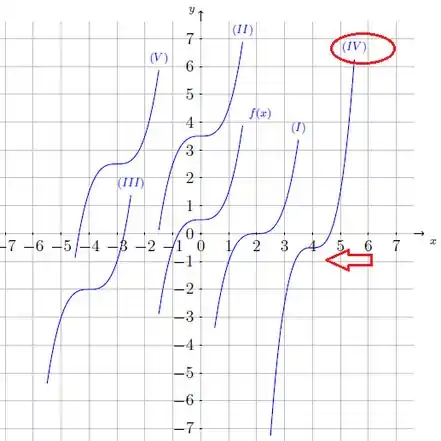
A curva , portanto, essa é a nossa resposta.
É isso, galera! Encerramos o exercício! 😉