UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 20
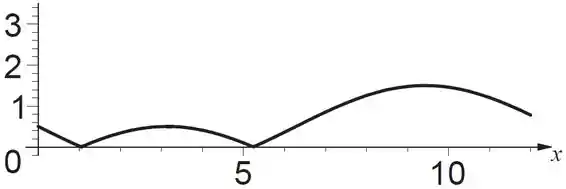
Determine o domínio, a imagem e esboce o gráfico da função dada.
Passo 1
Bom, o domínio é fácil, ele já deu!
Passo 2
E pra achar a imagem dessa função também vai ser fácil, basta dar um enquadro nela a partir do seno:
Muita calma na hora de aplicar o módulo.... Podemos ver que:
E pela definição de módulo, temos que:
Ou seja:
A imagem de é o intervalo .
Passo 3
Agora podemos focar no esboço!
Como sempre que nos deparamos com um módulo, a primeira a coisa a fazer é se livrar dele. Não tem que ter pena não, acaba com todos esses módulos.
Então vejamos quando a inequação abaixo é respeitada:
Passo 4
Agora vamos dar uma visualizada no círculo trigonométrico:
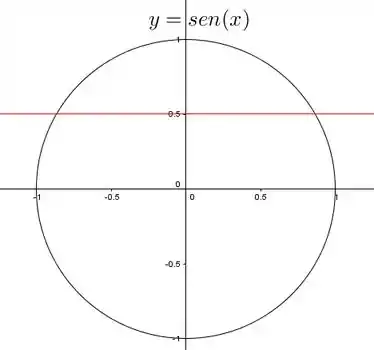
Temos que
Com
Passo 5
Detalhe que a função é definida em . Então também temos que considerar que
Portanto, considerando todo o domínio da função:
Passo 6
Só que no caso queremos . Então temos que multiplicar os valores do intervalo por 2, aí fica:
Mas a função só é definida em . Para respeitar essa condição, temos que cortar o do intervalo, então só sobra :
Passo 7
Então temos que:
A partir disso podemos escrever a sem módulo:
Passo 8
Agora finalmente podemos partir pro esboço!
Basta pensar no gráfico da função seno e pensar em alguns pontos que façam parte da curva. Por exemplo,
Ou:
E assim por diante.
Enfim, o esboço do gráfico vai ficar assim:
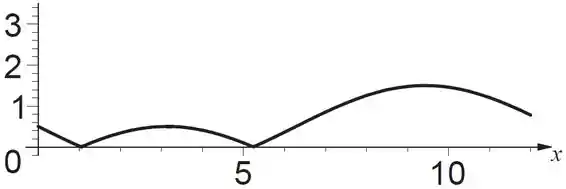
Resposta
Domínio:
Imagem:
