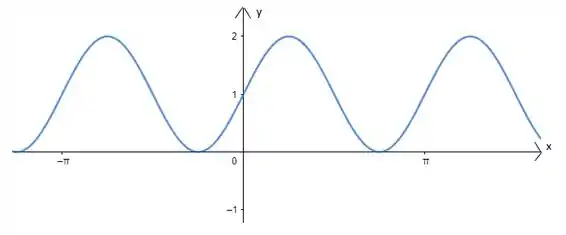
Faça o passo a passo de como construir o gráfico de a partir do gráfico de .
Passo 1
Opa! Bora lá!! Como o enunciado diz, precisamos partir do gráfico de :
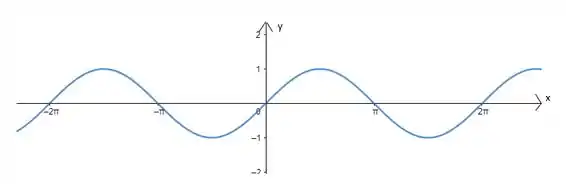
Beleza?!
Passo 2
Primeiro vamos multiplicar o por dentro do parêntenses. O que irá acontecer com o nosso gráfico quando fizermos isso? O período da função irá mudar! O período pode ser calculado por
Sendo o que multiplica o ! Assim, como o número que está multiplicando o é o
Ou seja, estaremos encolhendo a nossa função em 2 vezes no eixo :
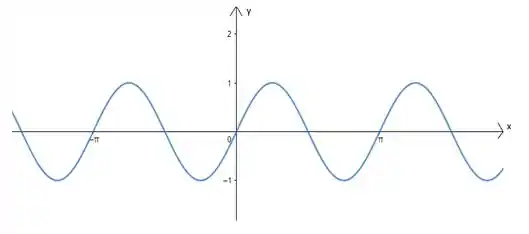
Passo 3
Agora falta somarmos 1 para chegarmos na função . E o que vai acontecer com o esboço do nosso gráfico quando fizermos isso?
Repare que estamos somando novamente um número, porém estamos somando fora do parêntese agora. Temos algo do tipo . Então o gráfico irá se deslocar para cima ou para baixo.
Aqui como estamos somando, o gráfico irá deslocar para cima! Então, teremos
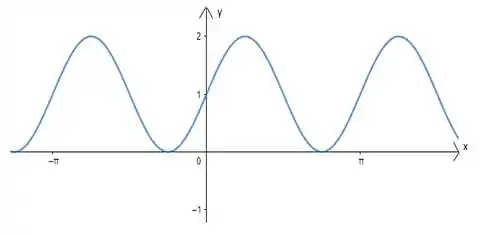
E assim conseguimos fazer o esboço da função !!!
Resposta