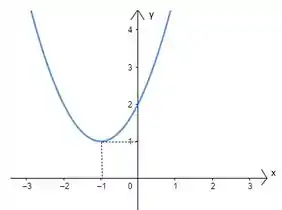
Esboce o gráfico da função
Partindo do gráfico da função
Passo 1
Vamos lá!! O enunciado já nos dá a dica de que devemos começar a esboçar o gráfico da função a partir da função ! Então vamos lá!!
A função tem essa carinha aqui:
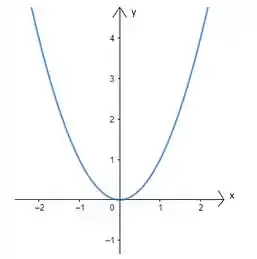
Beleza?!
Passo 2
Agora vamos fazer algo do tipo . Ou seja, onde é na função vai virar . Então a função vai ficar com essa carinha . Tá... mas o que acontece com o gráfico nesse caso?

Quando temos uma transformação do tipo essa transformação acontece no eixo horizontal, porque estamos mexendo com a variável . Então temos a possibilidade dele andar para a direita e para a esquerda.
Como estamos somando , deslocaremos unidades para a esquerda!
Perceba que na hora de fazer esse deslocamento no eixo , fazemos sempre ao contrário. Se estivermos somando , andamos unidade para trás, e se estivermos subtraindo , andamos unidade para frente. Assim, nosso gráfico se torna:
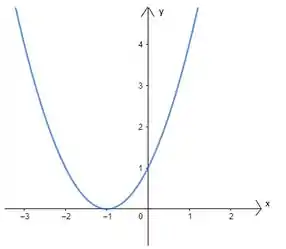
Ou seja, já temos o esboço da função !
Passo 3
Agora falta somarmos 1 para chegarmos na função .
E o que vai acontecer com o esboço do nosso gráfico quando fizermos isso?
Repare que estamos somando novamente um número, porém agora estamos somando fora dos parênteses.
Temos algo do tipo . Nesse caso, o gráfico irá se deslocar para cima ou para baixo.

Aqui como estamos somando, o gráfico irá deslocar para cima! Então, teremos
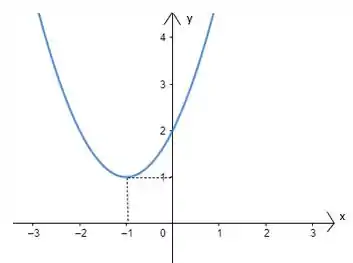
E assim conseguimos fazer o esboço da função !!! Uhulll!!
Resposta